
【题目】在△ABC中,AB=AC,点D是BC的中点,点E是AD上任意一点.
(1)如图1,连接BE、CE,问:BE=CE成立吗?并说明理由;
(2)如图2,若∠BAC=45°,BE的延长线与AC垂直相交于点F时,问:EF=CF成立吗?并说明理由.

【答案】(1)成立.(2)成立.见解析
【解析】
试题分析:(1)成立,根据等腰三角形的性质就可以求出∠BAE=∠CAE,再证明△ABE≌△ACE就可以得出结论;
(2)成立,由BF⊥AC,∠BAC=45°就可以求出AF=BF,在由条件证明△AEF≌△BCF就可以得出结论.
解:(1)成立.
理由:
∵AB=AC,D是BC的中点,∴∠BAE=∠CAE.
在△ABE和△ACE中,
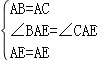
∴△ABE≌△ACE( SAS )
∴BE=CE.
(2)成立.
理由:
∵∠BAC=45°,BF⊥AF.
∴△ABF为等腰直角三角形
∴AF=BF…
由(1)知AD⊥BC,
∴∠EAF=∠CBF
在△AEF和△BCF中,
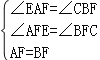 .
.
∴△AEF≌△BCF( AAS ),
∴EF=CF.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】暑假期间,两名教师计划带领若干名学生去旅游,他们联系了报价均为每人500元的两家旅行社![]() 经协商,甲旅行社的优惠条件是:两名教师全额收费,学生都按七折收费;乙旅行社的优惠条件是:教师、学生都按八折收费
经协商,甲旅行社的优惠条件是:两名教师全额收费,学生都按七折收费;乙旅行社的优惠条件是:教师、学生都按八折收费![]() 请你帮他们选择一下,选哪家旅行社比较合算.
请你帮他们选择一下,选哪家旅行社比较合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一张纸对折1次后,就得到2层;对折2次后,就得到4层;对折3次后,就得到8层;……,按照这样对折下去.
(1)求将一张纸对折6次后,层数是多少?
(2)求将一张纸对折n次后,层数是多少(用含n的式子表示)?
(3)若一张纸的厚度均为0.5mm,求将该纸张对折2018次后的总的厚度是多少mm?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
餐桌 | a | 270 | 500元 |
餐椅 | a﹣110 | 70 |
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有甲、乙两个容器,分别装有进水管和出水管,两容器的进、出水速度不变,先打开乙容器的进水管,2分钟时再打开甲容器的进水管,又过2分钟关闭甲容器的进水管,再过4分钟同时打开甲容器的进、出水管.直到12分钟时,同时关闭两容器的进、出水管.打开和关闭水管的时间忽略不计.容器中的水量y(升)与乙容器注水时间x(分)之间的关系如图所示.
(1)求甲容器的进、出水速度;
(2)甲容器的进、出水管都关闭后,是否存在两容器的水量相等?若存在,求出此时的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
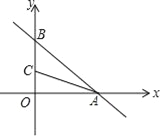
【题目】在平面直角坐标系中,已知一次函数y=﹣![]() x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )
x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )
A. (0,3) B. (0,![]() ) C. (0,
) C. (0,![]() ) D. (0,
) D. (0,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com