
【题目】如图,已知数轴上的点A表示的数为6,点B表示的数为﹣4,点C到点A、点B的距离相等,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为x(x大于0)秒.
(1)点C表示的数是 ;
(2)当x= 秒时,点P到达点A处?
(3)运动过程中点P表示的数是 (用含字母x的式子表示);
(4)当P,C之间的距离为2个单位长度时,求x的值.
![]()
【答案】(1)1(2)当x=5秒时,点P到达点A处(3)2x﹣4(4)当x等于1.5或3.5秒时,P、C之间的距离为2个单位长度
【解析】
(1)根据题意得到点C是AB的中点;
(2)、(3)根据点P的运动路程和运动速度列出方程;
(4)分两种情况:点P在点C的左边有右边.
(1)依题意得,点C是AB的中点,故点C表示的数是:![]() =1.
=1.
故答案为:1;
(2)[6﹣(﹣4)]÷2=10÷2=5(秒)
答:当x=5秒时,点P到达点A处.
(3)点P表示的数是2x﹣4.
故答案是:2x﹣4;
(4)当点P在点C的左边时,2x=3,则x=1.5;
当点P在点C的右边时,2x=7,则x=3.5.
综上所述,当x等于1.5或3.5秒时,P、C之间的距离为2个单位长度.


科目:初中数学 来源: 题型:
【题目】如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是( )
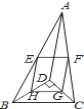
A. 7 B. 8 C. 11 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45° 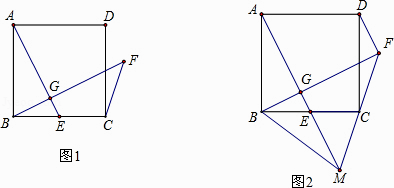
(1)求证:AG=FG;
(2)如图2延长FC、AE交于点M,连接DF、BM,若C为FM中点,BM=10,求FD的长. 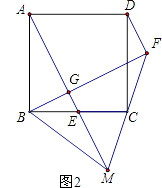
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A、B、C的坐标分别为(﹣1,0),(5,0),(0,2).若点P从A点出发,沿x轴正方向以每秒1个单位长度的速度向B点移动,连接PC并延长到点E,使CE=PC,将线段PE绕点P顺时针旋转90°得到线段PF,连接FB.若点P在移动的过程中,使△PBF成为直角三角形,则点F的坐标是 . 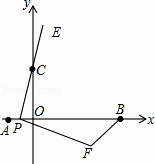
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB⊥AC,AB=2,AC=4.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转α°,分别交直线BC、AD于点E、F.

(1)当α= °,四边形ABEF是平行四边形;
(2)在旋转的过程中,从A、B、C、D、E、F中任意4个点为顶点构造四边形.
①α= °,构造的四边形是菱形;
②若构造的四边形是矩形,求出该矩形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知矩形ABCD,E为AD边上一动点,过A,B,E三点作⊙O,P为AB的中点,连接OP, 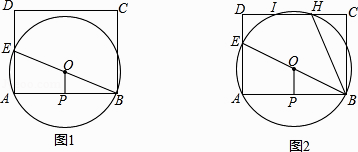
(1)求证:BE是⊙O的直径且OP⊥AB;
(2)若AB=BC=8,AE=6,试判断直线DC与⊙O的位置关系,并说明理由;
(3)如图2,若AB=10,BC=8,⊙O与DC边相交于H,I两点,连结BH,当∠ABE=∠CBH时,求△ABE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市水果批发部门欲将A市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为200元/时,其他主要参考数据如下:
运输工具 | 途中平均速度 (千米/时) | 运费 (元/千米) | 装卸费用 (元) |
火车 | 100 | 15 | 2000 |
汽车 | 80 | 20 | 900 |
(1)如果选择汽车的总费用比选择火车的总费用多1100元,那么你知道本市与A市之间的路程是多少千米吗?请你列方程解答;
(2)若A市与某市之间的路程为s千米,且知道火车与汽车在路上耽误的时间分别为2小时和3.1小时,要想将这批水果运往该市进行销售,则当s为多少时,选择火车和汽车运输所需费用相同?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有三个内角相等凸四边形叫三等角四边形.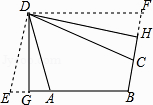
(1)三等角四边形ABCD中,∠A=∠B=∠C,求∠A的取值范围;
(2)如图,折叠平行四边形纸片DEBF,使顶点E,F分别落在边BE,BF上的点A,C处,折痕分别为DG,DH.求证:四边形ABCD是三等角四边形.
(3)三等角四边形ABCD中,∠A=∠B=∠C<90°,若CB=CD=4,则当AD的长为何值时,AB的长最大,其最大值是多少?(作图解答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com