
【题目】如图,直线l1:y=kx+b平行于直线y=x﹣1,且与直线l2: ![]() 相交于点P(﹣1,0).
相交于点P(﹣1,0).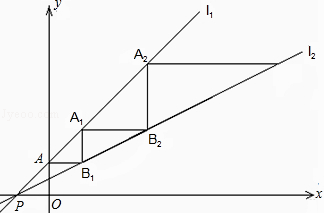
(1)求直线l1、l2的解析式;
(2)直线l1与y轴交于点A.一动点C从点A出发,先沿平行于x轴的方向运动,到达直线l2上的点B1处后,改为垂直于x轴的方向运动,到达直线l1上的点A1处后,再沿平行于x轴的方向运动,到达直线l2上的点B2处后,又改为垂直于x轴的方向运动,到达直线l1上的点A2处后,仍沿平行于x轴的方向运动,…
照此规律运动,动点C依次经过点B1 , A1 , B2 , A2 , B3 , A3 , …,Bn , An , …
①求点B1 , B2 , A1 , A2的坐标;
②请你通过归纳得出点An、Bn的坐标;并求当动点C到达An处时,运动的总路径的长?
【答案】
(1)
解:∵y=kx+b平行于直线y=x﹣1,
∴y=x+b
∵过P(﹣1,0),
∴﹣1+b=0,
∴b=1
∴直线l1的解析式为y=x+1;
∵点P(﹣1,0)在直线l2上,
∴ ![]() ;
;
∴ ![]() ;
;
∴直线l2的解析式为 ![]()
(2)
解:①A点坐标为(0,1),
则B1点的纵坐标为1,设B1(x1,1),
∴ ![]() ;
;
∴x1=1;
∴B1点的坐标为(1,1);
则A1点的横坐标为1,设A1(1,y1)
∴y1=1+1=2;
∴A1点的坐标为(1,2),即(21﹣1,21);
同理,可得B2(3,2),A2(3,4),即(22﹣1,22);
②经过归纳得An(2n﹣1,2n),Bn(2n﹣1,2n﹣1);
当动点C到达An处时,运动的总路径的长为An点的横纵坐标之和再减去1,
即2n﹣1+2n﹣1=2n+1﹣2.
【解析】(1)根据直线l1:y=kx+b平行于直线y=x﹣1,求得k=1,再由与直线l2: ![]() 相交于点P(﹣1,0),分别求出b和m的值.(2)由直线l1的解析式,求出A点的坐标,从而求出B1点的坐标,依此类推再求得A1、B2、A2的值,从而得到An、Bn , 进而求出点C运动的总路径的长.
相交于点P(﹣1,0),分别求出b和m的值.(2)由直线l1的解析式,求出A点的坐标,从而求出B1点的坐标,依此类推再求得A1、B2、A2的值,从而得到An、Bn , 进而求出点C运动的总路径的长.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
餐桌 | a | 270 | 500元 |
餐椅 | a﹣110 | 70 |
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
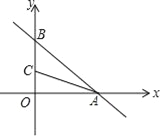
【题目】在平面直角坐标系中,已知一次函数y=﹣![]() x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )
x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )
A. (0,3) B. (0,![]() ) C. (0,
) C. (0,![]() ) D. (0,
) D. (0,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,切点为N,则DM的长为( ) 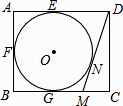
A.![]()
B.2 ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环保知识竞赛”,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频数分布直方图如下:

(1)直接写出a的值,并补全频数分布直方图.
分组 | 频数 | 频率 |
49.5~59.5 | 0.08 | |
59.5~69.5 | 0.12 | |
69.5~79.5 | 20 | |
79.5~89.5 | 32 | |
89.5~100.5 | a |
(2)若成绩在80分以上(含80分)为优秀,求这次参赛的学生中成绩为优秀的约为多少人?
(3)若这组被抽查的学生成绩的中位数是80分,请直接写出被抽查的学生中得分为80分的至少有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面一段文字,再回答后面的问题.
已知在平面直角坐标系内两点P1(x1,y1),P2(x2,y2),点P1,P2间的距离公式P1P2=![]() ,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可简化为|x2-x1|或|y2-y1|.
,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可简化为|x2-x1|或|y2-y1|.
(1)已知A(2,4),B(-3,-8),试求A,B两点间的距离;
(2)已知各顶点坐标为A(0,6),B(-3,2),C(3,2),你能判定△ABC的形状吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣ ![]() 与x轴、y轴分别交于点A、B;点Q是以C(0,﹣1)为圆心、1为半径的圆上一动点,过Q点的切线交线段AB于点P,则线段PQ的最小是 .
与x轴、y轴分别交于点A、B;点Q是以C(0,﹣1)为圆心、1为半径的圆上一动点,过Q点的切线交线段AB于点P,则线段PQ的最小是 . 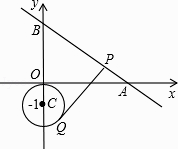
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),P6(2,0),…,则点P2018的坐标是________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com