
【题目】如图,直线y=﹣ ![]() 与x轴、y轴分别交于点A、B;点Q是以C(0,﹣1)为圆心、1为半径的圆上一动点,过Q点的切线交线段AB于点P,则线段PQ的最小是 .
与x轴、y轴分别交于点A、B;点Q是以C(0,﹣1)为圆心、1为半径的圆上一动点,过Q点的切线交线段AB于点P,则线段PQ的最小是 . 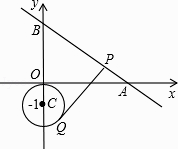
【答案】![]()
【解析】解:过点C作CP⊥直线AB于点P,过点P作⊙C的切线PQ,切点为Q,此时PQ最小,连接CQ,如图所示.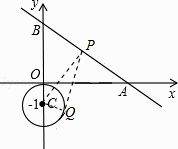
当x=0时,y=3,
∴点B的坐标为(0,3);
当y=0时,x=4,
∴点A的坐标为(4,0).
∴OA=4,OB=3,
∴AB= ![]() =5,
=5,
∴sinB= ![]() =
= ![]() .
.
∵C(0,﹣1),
∴BC=3﹣(﹣1)=4,
∴CP=BCsinB= ![]() .
.
∵PQ为⊙C的切线,
∴在Rt△CQP中,CQ=1,∠CQP=90°,
∴PQ= ![]() =
= ![]() .
.
故答案为: ![]() .
.
过点C作CP⊥直线AB与点P,过点P作⊙C的切线PQ,切点为Q,此时PQ最小,连接CQ,利用角的正弦求出CP的值,再根据勾股定理即可求出PQ的长度.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个,2个甲种部件和3个乙种部件配成一套,问加工甲、乙两种部件各安排多少人才能使每天加工的两种部件刚好配套?并求出加工了多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y=kx+b平行于直线y=x﹣1,且与直线l2: ![]() 相交于点P(﹣1,0).
相交于点P(﹣1,0).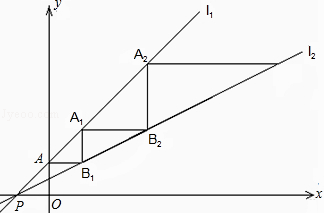
(1)求直线l1、l2的解析式;
(2)直线l1与y轴交于点A.一动点C从点A出发,先沿平行于x轴的方向运动,到达直线l2上的点B1处后,改为垂直于x轴的方向运动,到达直线l1上的点A1处后,再沿平行于x轴的方向运动,到达直线l2上的点B2处后,又改为垂直于x轴的方向运动,到达直线l1上的点A2处后,仍沿平行于x轴的方向运动,…
照此规律运动,动点C依次经过点B1 , A1 , B2 , A2 , B3 , A3 , …,Bn , An , …
①求点B1 , B2 , A1 , A2的坐标;
②请你通过归纳得出点An、Bn的坐标;并求当动点C到达An处时,运动的总路径的长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠BAC=90°,AB=AC,MN是经过点A的直线,BD⊥MN,CE⊥MN,垂足分别为D,E.
(1)求证:①∠BAD=∠ACE;②BD=AE.
(2)请写出BD,CE,DE三者间的数量关系式,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系xOy中,把从点P出发沿纵或横方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若P(﹣1,1),Q(2,3),则P,Q的“实际距离”为5,即PS+SQ=5或PT+TQ=5.环保低碳的共享单车,正式成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为A(3,1),B(5,﹣3),C(﹣1,﹣5),若点M表示单车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南宁市金陵镇三联村无公害蔬菜基地有甲、乙两种植户,他们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
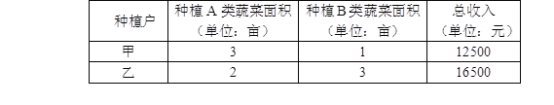
说明:不同种植户种植的同类蔬菜每亩平均收入相等.
(1)求A、B两类蔬菜每亩平均收入各是多少元?
(2)某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租种方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b的图象与反比例函数y= ![]() 的图象交于第二、四象限内的A、B两点,与y轴交于C点,过A作AH⊥y轴于H,OH=3,tan∠AOH=
的图象交于第二、四象限内的A、B两点,与y轴交于C点,过A作AH⊥y轴于H,OH=3,tan∠AOH= ![]() ,点B的坐标为(m,﹣2).
,点B的坐标为(m,﹣2). 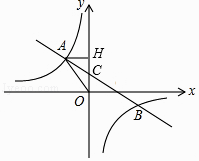
(1)求△AHO的周长;
(2)求反比例函数和一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC和Rt△DCB中,AB=DC,∠A=∠D=90°,AC与BD交于点O,则有△________≌△________,其判定依据是________,还有△________≌△________,其判定依据是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图数轴上两点A、B所别应的分别为﹣3、1,点P在数轴上从点A出发以每秒钟2个单位的长度的速度向右运动,点Q在数轴上从点B出发以每秒钟1个单位长度的速度向左运动,设点P的运动时间为t秒.
(1)直接写出线段AB的中点所对应的数及t秒后点P所对应的数.
(2)若点P和点Q同时出发,求点P和点Q相遇时的位置所对应的数;
(3)若点P比点Q迟1秒钟出发,问点P出发几秒后,点P和点Q刚好相距1个单位长度.并问此时数轴上是否存在一个点C,使其到点A、点P和点Q这三点的距离和最小?若存在,直接写出点C所对应的数;若不存在,试说明理由.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com