
【题目】商场服装柜在销售中发现:某童装平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元.为了迎接“六一”国际儿童节,商场决定采取适当的降价措施,调查发现:如果每件童装降价
元.为了迎接“六一”国际儿童节,商场决定采取适当的降价措施,调查发现:如果每件童装降价![]() 元,那么平均每天就可多售出
元,那么平均每天就可多售出![]() 件.要想平均每天销售这种童装共盈利
件.要想平均每天销售这种童装共盈利![]() 元,设每件童装降价
元,设每件童装降价![]() 元,那么应满足的方程是________.
元,那么应满足的方程是________.
科目:初中数学 来源: 题型:
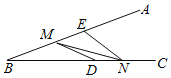
【题目】如图,∠ABC=20°,点D,E分别在射线BC,BA上,且BD=3,BE=3,点M,N分别是射线BA,BC上的动点,求DM+MN+NE的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成相应任务:



(1)小明在研究命题①时,在图1的正方形网格中画出两个符合条件的四边形.由此判断命题①是 命题(填“真”或“假”).
(2)小彬经过探究发现命题②是真命题.请你结合图2证明这一命题.
(3)小颖经过探究又提出了一个新的命题:“若![]() ,
,![]() ,
,![]() , , ,则四边形
, , ,则四边形![]() ≌四边形
≌四边形![]() ”请在横线上填写两个关于“角”的条件,使该命题为真命题.
”请在横线上填写两个关于“角”的条件,使该命题为真命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=3,M为边BC上的点,连接AM.如果将△ABM沿直线AM翻折后,点B恰好落在边AC的中点处,那么点M到AC的距离是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用同样规格的规格黑白两色正方形瓷砖铺设矩形地面,请观察图形并解答有关问题.

![]() 在第
在第![]() 个图中,每一横行共有________块瓷砖,每竖行共有________块瓷砖(均用含
个图中,每一横行共有________块瓷砖,每竖行共有________块瓷砖(均用含![]() 的代数式表示)
的代数式表示)
![]() 设铺设地面所用的瓷砖总块数
设铺设地面所用的瓷砖总块数![]() ,写出
,写出![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围)
的取值范围)
![]() 按上述铺设方案,铺一块这样的地面共用了
按上述铺设方案,铺一块这样的地面共用了![]() 块瓷砖,求此时
块瓷砖,求此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为了从甲、乙两同学中选出班长,进行了一次演讲答辩和民主测评,A、B、C、D、E五位老师作为评委,对演讲答辩得分进行评价,结果如演讲答辩得分表,另全班50位同学则参与民主测评进行投票,结集如图.
A | B | C | D | E | |
甲 | 90 | 92 | 94 | 95 | 88 |
乙 | 89 | 86 | 87 | 94 | 91 |

规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;民主测评得分=“好”票数×2分+“较好“票数×1分+“一般”票数×0分.
(1)求甲、乙两位选手各自演讲答辩的得分
(2)求甲、乙两位选手各自民主测评的得分
(3)若演讲答辩得分和民主测评得分按2∶3的权重比计算两位选手的综合得分,则应选取哪位选手当班长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球运动员去年共参加![]() 场比赛,其中
场比赛,其中![]() 分球的命中率为
分球的命中率为![]() ,平均每场有
,平均每场有![]() 次
次![]() 分球未投中.
分球未投中.
![]() 该运动员去年的比赛中共投中多少个
该运动员去年的比赛中共投中多少个![]() 分球?
分球?
![]() 在其中的一场比赛中,该运动员
在其中的一场比赛中,该运动员![]() 分球共出手
分球共出手![]() 次,小明说,该运动员这场比赛中一定投中了
次,小明说,该运动员这场比赛中一定投中了![]() 个
个![]() 分球,你认为小明的说法正确吗?请说明理由.
分球,你认为小明的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运30kg,A型机器人搬运900kg与B型机器人搬运600kg所用时间相等,两种机器人每小时分别搬运多少化工原料?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com