
����Ŀ��ij������˾�Ŀ�ݳ��ͻ���ͬʱ�Ӽس������Ը��Ե��ٶ��������ҵ���ʻ����ݳ������ҵغ�ж����Ʒ����װ���ﹲ��45���ӣ�������ԭ·����һ�ٶ����ٷ��أ�ֱ���������������֪�������ٶ�Ϊ60ǧ��/ʱ������֮��ľ���y��ǧ�ף��������ʻʱ��x��Сʱ��֮��ĺ���ͼ����ͼ��ʾ.

��������4�����ۣ�
�ٿ�ݳ��Ӽص��ҵص��ٶ�Ϊ100ǧ��/Сʱ��
�ڼס�������֮��ľ���Ϊ120ǧ�ף�
��ͼ�е�B������Ϊ(3.75,75)��
�ܿ�ݳ����ҵط���ʱ���ٶ�Ϊ90ǧ��/Сʱ
���Ͻ�����ȷ����________________��
���𰸡��٢ۢ�
����������������������ݳ��Ӽص��ҵص��ٶ�Ϊxǧ��/ʱ����3��x��60��=120��x=100����������ȷ����
����Ϊ120ǧ���ǿ�ݳ������ҵغ�����֮��ľ��룬���Ǽס�������֮��ľ��룬����������
����Ϊ��ݳ������ҵغ�������Ʒ����װ���ﹲ��45���ӣ�����ͼ�е�B�ĺ�����Ϊ3+![]() =
=![]() ��������Ϊ120��60��
��������Ϊ120��60��![]() =75����������ȷ����
=75����������ȷ����
�����ݳ����ҵط���ʱ���ٶ�Ϊyǧ��/ʱ����y+60����![]() ��=75��y=90����������ȷ����
��=75��y=90����������ȷ����
�ʴ�Ϊ���٢ۢ���


 С��ʿ��ĩ����100��ϵ�д�
С��ʿ��ĩ����100��ϵ�д� ��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�����ǰ����һ��ʹֱ�ǵĶ����غ��ڵ�O��![]() ���ֵΪ�� ����
���ֵΪ�� ����

A. С��180�� B. ����180�� C. ����180�� D. ����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
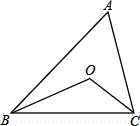
����Ŀ����ͼ����![]() ABC�У�BO��CO�ֱ�ƽ�֡�ABC�͡�ACB�����㣺
ABC�У�BO��CO�ֱ�ƽ�֡�ABC�͡�ACB�����㣺
��1������A ![]() 60�������BOC�Ķ�����
60�������BOC�Ķ�����
��2������A ![]() 100��, ���BOC�Ķ����Ƕ��٣�
100��, ���BOC�Ķ����Ƕ��٣�
��3������A ![]() 120��, ���BOC�Ķ������Ƕ��٣�
120��, ���BOC�Ķ������Ƕ��٣�
��4���ɣ�1������2������3�����㷢����ʲô���ɣ�����һ����ʽ��������ɱ�ʾ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB��O��ֱ������C��O�ϣ�����C��ֱ����AB���ӳ��߽��ڵ�P��AC=PC����COB=2��PCB.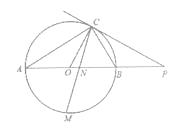
��1����֤��PC��O�����ߣ�
��2����֤��BC= ![]() AB��
AB��
��3����M�ǻ�AB���е㣬CM��AB�ڵ�N����AB=4����MN��MC��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC��ֽƬ����ͼ��ʾ�ķ�ʽ�۵���ʹ��B���ڱ�AC�ϣ���Ϊ��B�䣬�۵���ΪEF����֪AB=AC=8��BC=10�����Ե�B�䡢F��CΪ��������������ABC���ƣ���ôBF�ij����� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��д�����������еĹ�ϵʽ����ָ�����еı����ͳ�����
��1��ֱ����������һ�����a����һ�������֮��Ĺ�ϵ��
��2��һʢ��30��ˮ��ˮ�䣬ÿСʱ����0.5��ˮ��������ˮʱ��t��Сʱ����ʾˮ���е�ʣˮ��y���֣���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���������������ϴ������е�A��B��C������AB=2��BC=1����ͼ��ʾ�����A��B��C����Ӧ���ĺ���p��

��1������BΪԭ�㣬д����A��C����Ӧ������������p��ֵ������CΪԭ�㣬p���Ƕ��٣�
��2����ԭ��O��ͼ�������ϵ�C���ұߣ���CO=28����p��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A��0��1������B��0��1+t����C��0��1��t����t��0������P����D��3��3��ΪԲ�ģ�1Ϊ�뾶��Բ���˶�����ʼ�������BPC=90�㣬��t����Сֵ�� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ����ֱ�Ĺ�·l������ԭ����·����һ����վA�����빫·5 ![]() ǧ�ĵط���һ�����B��A��B��ֱ�߾�����10
ǧ�ĵط���һ�����B��A��B��ֱ�߾�����10 ![]() ǧ�ף�һ�죬�����B�Ż�����Ա������ǰ���Ȼ����������ڹ�·�ϵ�����ٶ���80ǧ��/Сʱ�����ڲݵ��ϵ�����ٶ���40ǧ��/Сʱ�����������ڳ�������쾭��Сʱ�ɵ�������B�����������ѣ��������ɴӹ�·������λ�ý���ݵ���ʻ����
ǧ�ף�һ�죬�����B�Ż�����Ա������ǰ���Ȼ����������ڹ�·�ϵ�����ٶ���80ǧ��/Сʱ�����ڲݵ��ϵ�����ٶ���40ǧ��/Сʱ�����������ڳ�������쾭��Сʱ�ɵ�������B�����������ѣ��������ɴӹ�·������λ�ý���ݵ���ʻ���� 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com