
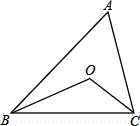
【题目】如图,在![]() ABC中,BO、CO分别平分∠ABC和∠ACB.计算:
ABC中,BO、CO分别平分∠ABC和∠ACB.计算:
(1)若∠A ![]() 60°,求∠BOC的度数;
60°,求∠BOC的度数;
(2)若∠A ![]() 100°, 则∠BOC的度数是多少?
100°, 则∠BOC的度数是多少?
(3)若∠A ![]() 120°, 则∠BOC的度数又是多少?
120°, 则∠BOC的度数又是多少?
(4)由(1)、(2)、(3),你发现了什么规律?请用一个等式将这个规律表示出来.
【答案】(1)∠BOC![]() 120°;(2)∠BOC
120°;(2)∠BOC![]() 140°;(3)∠BOC=150°;(4)∠BOC=90°+
140°;(3)∠BOC=150°;(4)∠BOC=90°+![]() ∠A
∠A
【解析】
(1)根据BO、CO分别平分∠ABC和∠ACB可得: ∠CBO+∠BCO的值,再根据三角形内角和得出∠BOC;
(2)、(3)同理(1)可求得;
(4)根据(1)-(3)规律可得.
(1)∵BO、CO分别平分∠ABC和∠ACB.∠A ![]() 600
600
∴∠CBO+∠BCO![]()
![]() (1800
(1800![]() ∠A)
∠A)![]()
![]() (1800
(1800![]() 600)
600)![]() 600
600
∴∠BOC![]() 1800
1800![]() (∠CBO+∠BCO)
(∠CBO+∠BCO)![]() 1800
1800![]() 600
600![]() 1200
1200
(2)同理,若∠A ![]() 1000, 则∠BOC
1000, 则∠BOC![]() 1800
1800![]()
![]() (1800
(1800![]() ∠A)
∠A)![]() 900+
900+![]() ∠A
∠A![]() 1400
1400
(3)同理,若∠A ![]() 1200, 则∠BOC
1200, 则∠BOC![]() 1800
1800![]()
![]() (1800
(1800![]() ∠A)
∠A)![]() 900+
900+![]() ∠A
∠A![]() 1500
1500
(4)由(1)、(2)、(3),发现:∠BOC![]() 1800
1800![]()
![]() (1800
(1800![]() ∠A)
∠A)![]() 900+
900+![]() ∠A
∠A


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4cm,AD=12cm,P点在AD边上以每秒1cm的速度从A向D运动,点Q在BC边上,以每秒4cm的速度从C点出发,在CB间往返运动,二点同时出发,待P点到达D点为止,在这段时间内,线段PQ有( )次平行于AB.

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
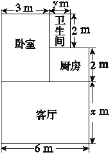
【题目】丁丁家买了一套安置房,地面结构如图所示.
(1)写出用含x、y的式子表示地面的总面积;
(2)如果x=4 m,y=1.5 m,铺1 m2地砖的平均费用为80元,求铺地砖的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明有5张写着不同的数字的卡片,请你按要求抽出卡片,完成下列各问题:
![]()
(1)从中取出2张卡片,使这2张卡片上数字乘积最大,最大值是 ;
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,最小值是 ;
(3)从中取出4张卡片,用学过的运算方法,使结果为24.写出运算式子:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点△ABC(顶点是网格线的交点的三角形)的顶点A(-4,5),C(-1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系,并计算△ABC的面积;
(2)作出△ABC关于y轴对称的△A′B′C′;
(3)点P在x轴上,且△POB的面积等于△ABC面积的一半,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=4,BC=5,点E在边CD上,以B为坐标原点,BA所在直线为y轴,BC所在直线为x轴,建立平面直角坐标系,A(0,4).以AE所在直线为折痕折叠长方形ABCD,点D恰好落在BC边上的F点.

(1)求点F的坐标;
(2)求点E的坐标;
(3)在AE上是否存在点P,使PB+PF最小?若存在,作出点P的位置,并求出PB+PF的最小值;不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示.

现有以下4个结论:
①快递车从甲地到乙地的速度为100千米/小时;
②甲、乙两地之间的距离为120千米;
③图中点B的坐标为(3.75,75);
④快递车从乙地返回时的速度为90千米/小时
以上结论正确的是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2008年5月12日四川汶川地区发生8.0级特大地震.举国上下通过各种方式表达爱心.某企业决定用p万元援助灾区n所学校,用于搭建帐篷和添置教学设备.根据各校不同的受灾情况,该企业捐款的分配方案是:所有学校得到的捐款数都相等,到第n所学校时捐款恰好分完,捐款的分配方法如下表所示.(其中p,n,a都是正整数)根据以上信息,解答下列问题:
(1)写出p与n的关系式;
(2)当p=125时,该企业能援助多少所学校?
(3)根据震区灾情,该企业计划再次提供不超过20a万元的捐款,按照原来的分配方案援助其它学校.若a由(2)确定,则再次提供的捐款最多又可以援助多少所学校?
分配顺序 | 分配数额(单位:万元) | |
帐篷费用 | 教学设备费用 | |
第1所学校 | 5 | 剩余款的 |
第2所学校 | 10 | 再剩余款的 |
第3所学校 | 15 | 再剩余款的 |
… | … | … |
第(n﹣1)所学校 | 5(n﹣1) | 再剩余款的 |
第n所学校 | 5n | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com