
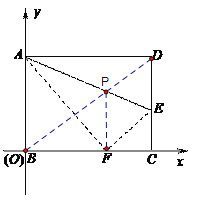
����Ŀ����ͼ���ڳ�����ABCD�У�AB��4��BC��5����E�ڱ�CD�ϣ���BΪ����ԭ�㣬BA����ֱ��Ϊy�ᣬBC����ֱ��Ϊx�ᣬ����ƽ��ֱ������ϵ��A(0��4)����AE����ֱ��Ϊ�ۺ��۵�������ABCD����Dǡ������BC���ϵ�F�㣮

(1)���F�����ꣻ
(2)���E�����ꣻ
(3)��AE���Ƿ���ڵ�P��ʹPB��PF��С�������ڣ�������P��λ�ã������PB��PF����Сֵ�������ڣ�˵�����ɣ�
���𰸡�(1)F (3��0) �� (2) E(5�� ![]() )�� (3) ��BD��AE����P�����P�����������ĵ㣻
)�� (3) ��BD��AE����P�����P�����������ĵ㣻 ![]()
����������������� ![]() �����۵������ʣ��ɵ�
�����۵������ʣ��ɵ�![]() ��
��![]() �У����ݹ��ɶ������
�У����ݹ��ɶ������![]() �ij������������
�ij������������![]() ������.
������.
![]() ��
��![]() ��
��![]()
![]() ��
��![]() �У����ݹ��ɶ������г����̣����
�У����ݹ��ɶ������г����̣����![]() ��ֵ�����������
��ֵ�����������![]() ������.
������.
![]() ��
��![]() ����
����![]() �ĶԳƵ��ǵ�
�ĶԳƵ��ǵ�![]() ,��BD��AE����P�����P�����������ĵ㣻
,��BD��AE����P�����P�����������ĵ㣻
���ݹ��ɶ������![]() �ó��ȼ���.
�ó��ȼ���.
��������� ![]() ������ABCD��
������ABCD��
![]()
�����۵������ʣ��ɵ�![]()
��![]() ��
�У� ![]()
![]() ��
��![]() ��������
�������� ![]()
![]() ��
��![]() ��
��![]()
![]()
��![]() ��
�У�
![]()
���� ![]()
��ã� ![]()
![]() ��
��![]() ��������
�������� ![]()
![]() ��
��![]() ����
����![]() �ĶԳƵ��ǵ�
�ĶԳƵ��ǵ�![]() ,��BD��AE����P�����P�����������ĵ㣻��ͼ��ʾ��
,��BD��AE����P�����P�����������ĵ㣻��ͼ��ʾ��
��ʱ![]()


 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ƽ���ı���ABCD����M��N�ֱ��ڱ�AD�ͱ�BC�ϣ���E��F���߶�BD�ϣ���AM=CN��DF=BE����֤��
��1����DFM=��BEN��
��2���ı���MENF��ƽ���ı��Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ǵij��д����˼���ķ��㣮��ͼ������г�š������г����κ����С��������ʱ��С�����֧�ܵĵ�N�����涥��M�ľ���MN=75cm���ҿ��Կ�������洹ֱ��չ��С����ʹ���汣��ˮƽ��AB��MN����MAB=��MNB=37�㣬��֧�ܳ�BN�������AB�ij���֮�͵���MN�ij��ȣ���С��������Ŀ���AB�������ȷ��1cm���ο����ݣ�sin37���0.6��cos37���0.8��tan37���0.75��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
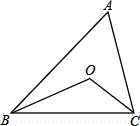
����Ŀ����ͼ����![]() ABC�У�BO��CO�ֱ�ƽ�֡�ABC�͡�ACB�����㣺
ABC�У�BO��CO�ֱ�ƽ�֡�ABC�͡�ACB�����㣺
��1������A ![]() 60�������BOC�Ķ�����
60�������BOC�Ķ�����
��2������A ![]() 100��, ���BOC�Ķ����Ƕ��٣�
100��, ���BOC�Ķ����Ƕ��٣�
��3������A ![]() 120��, ���BOC�Ķ������Ƕ��٣�
120��, ���BOC�Ķ������Ƕ��٣�
��4���ɣ�1������2������3�����㷢����ʲô���ɣ�����һ����ʽ��������ɱ�ʾ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A��B������ֱ�Ϊ��-2,3���ͣ�1,3����������y=ax2+bx+c��a<0���Ķ������߶�AB���˶�ʱ����״���ֲ��䣬����x�ύ��C��D���㣨C��D����ࣩ���������н��ۣ���c<3���ڵ�x<-3ʱ��y��x���������������D�ĺ��������ֵΪ5�����C�ĺ�������СֵΪ-5���ܵ��ı���ACDBΪƽ���ı���ʱ��a= ![]() .������ȷ���ǣ� ��
.������ȷ���ǣ� ��
A.�ڢ�
B.�ڢ�
C.�٢ۢ�
D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB��O��ֱ������C��O�ϣ�����C��ֱ����AB���ӳ��߽��ڵ�P��AC=PC����COB=2��PCB.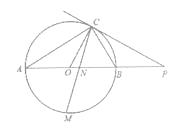
��1����֤��PC��O�����ߣ�
��2����֤��BC= ![]() AB��
AB��
��3����M�ǻ�AB���е㣬CM��AB�ڵ�N����AB=4����MN��MC��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC��ֽƬ����ͼ��ʾ�ķ�ʽ�۵���ʹ��B���ڱ�AC�ϣ���Ϊ��B�䣬�۵���ΪEF����֪AB=AC=8��BC=10�����Ե�B�䡢F��CΪ��������������ABC���ƣ���ôBF�ij����� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���������������ϴ������е�A��B��C������AB=2��BC=1����ͼ��ʾ�����A��B��C����Ӧ���ĺ���p��

��1������BΪԭ�㣬д����A��C����Ӧ������������p��ֵ������CΪԭ�㣬p���Ƕ��٣�
��2����ԭ��O��ͼ�������ϵ�C���ұߣ���CO=28����p��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ������y=ax2+bx+c������ʽ����ȷ���ǣ� �� 
A.a+b+c��0
B.b2��4ac��0
C.c��2b
D.abc��0
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com