
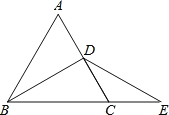
【题目】已知△ABC为等边三角形,BD为△ABC的高,延长BC至E,使CE=CD=1,连接DE,则BE=___________,∠BDE=_________ .
科目:初中数学 来源: 题型:
【题目】已知,关于x的一元二次方程x2+(1﹣k)x﹣k=0 (其中k为常数).
(1)判断方程根的情况并说明理由;
(2)若﹣1<k<0,设方程的两根分别为m,n(m<n),求它的两个根m和n;
(3)在(2)的条件下,若直线y=kx﹣1与x轴交于点C,x轴上另两点A(m,0)、点B(n,0),试说明是否存在k的值,使这三点中相邻两点之间的距离相等?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.

(1)求证:CF=DG;
(2)求出∠FHG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三学生小丽、小杰为了解本校初二学生每周上网的时间,各自在本校进行了抽样调查.小丽调查了初二电脑爱好者中![]() 名学生每周上网的时间,算得这些学生平均每周上网时间为
名学生每周上网的时间,算得这些学生平均每周上网时间为![]() 小时;小杰从全体
小时;小杰从全体![]() 名初二学生名单中随机抽取了
名初二学生名单中随机抽取了![]() 名学生,调查了他们每周上网的时间,算得这些学生平均每周上网时间为
名学生,调查了他们每周上网的时间,算得这些学生平均每周上网时间为![]() 小时.小丽与小杰整理各自样本数据,如下表所示.
小时.小丽与小杰整理各自样本数据,如下表所示.
时间段(小时/周) | 小丽抽样人数 | 小杰抽样人数 |
|
|
|
|
|
|
|
|
|
|
|
|
(每组可含最低值,不含最高值)
请根据上述信息,回答下列问题:

![]() 你认为哪位学生抽取的样本具有代表性?答:________;估计该校全体初二学生平均每周上网时间为________小时;
你认为哪位学生抽取的样本具有代表性?答:________;估计该校全体初二学生平均每周上网时间为________小时;
![]() 根据具有代表性的样本,把上图中的频数分布直方图补画完整;
根据具有代表性的样本,把上图中的频数分布直方图补画完整;
![]() 在具有代表性的样本中,中位数所在的时间段是________小时/周;
在具有代表性的样本中,中位数所在的时间段是________小时/周;
![]() 专家建议每周上网
专家建议每周上网![]() 小时以上(含
小时以上(含![]() 小时)的同学应适当减少上网的时间,根据具有代表性的样本估计,该校全体初二学生中有多少名同学应适当减少上网的时间?
小时)的同学应适当减少上网的时间,根据具有代表性的样本估计,该校全体初二学生中有多少名同学应适当减少上网的时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,OA=OC,则由抛物线的特征写出如下含有a、b、c三个字母的等式或不等式:①![]() =﹣1;②ac+b+1=0;③abc>0;④a﹣b+c>0.其中正确的个数是( )
=﹣1;②ac+b+1=0;③abc>0;④a﹣b+c>0.其中正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A,B两点,与y轴交于C点,且A(﹣1,0).
与x轴交于A,B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)点M是对称轴上的一个动点,当MA+MC的值最小时,求点M的坐标。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com