
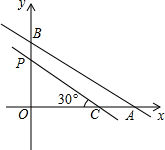
 如图,在直角坐标系中,一次函数在y轴上的交点坐标是B(0,5),与x轴交于点A的横坐标是图象与y轴交点到原点距离的2倍,点C的坐标是(6,0),点P的坐标是(0,y)
如图,在直角坐标系中,一次函数在y轴上的交点坐标是B(0,5),与x轴交于点A的横坐标是图象与y轴交点到原点距离的2倍,点C的坐标是(6,0),点P的坐标是(0,y)分析 (1)由B的坐标及一次函数与x轴交于点A的横坐标是图象与y轴交点到原点距离的2倍,确定出A的坐标,得到OA与OB的长,再由C与P的坐标确定出OP与OC的长,四边形ABPC面积等于三角形AOB面积减去三角形POC面积,列出S关于y的函数解析式,并求出y的范围即可;
(2)根据∠PCO的度数,以及OC的长,求出OP的长,确定出y的值,代入(2)中计算即可求出S的值.
解答 解:(1)∵一次函数在y轴上的交点坐标是B(0,5),与x轴交于点A的横坐标是图象与y轴交点到原点距离的2倍,
∴A(10,0),即OA=10,OB=5,
∵C(6,0),P(0,y),
∴OP=y,OC=6,
∴S=S四边形ABPC=$\frac{1}{2}$OA•OB-$\frac{1}{2}$OP•OC=$\frac{1}{2}$×10×5-$\frac{1}{2}$×y×6=25-3y(0<y<5);
(2)∵∠PCO=30°,OC=6,
∴tan30°=$\frac{OP}{OC}$,即OP=OCtan30°=6×$\frac{\sqrt{3}}{3}$=2$\sqrt{3}$,
则S=S四边形ABPC=25-6$\sqrt{3}$.
点评 此题属于一次函数综合题,涉及的知识有:坐标与图形性质,三角形面积公式,以及锐角三角函数定义,熟练掌握一次函数性质是解本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ax2+bx+c=0 | B. | 2x2+3x=2x(x-1) | C. | (k2+1)x2-2x=6 | D. | x2-$\frac{5}{x}$+1=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
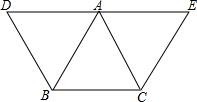 如图所示,已知BD∥AC,CE∥BA,且点D、A、E在一条直线上,设∠BAC=x,∠D+∠E=y.
如图所示,已知BD∥AC,CE∥BA,且点D、A、E在一条直线上,设∠BAC=x,∠D+∠E=y.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com