
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(![]() )和B(4,6),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,6),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)当C为抛物线顶点的时候,求![]() 的面积.
的面积.
(3)是否存在质疑的点P,使![]() 的面积有最大值,若存在,求出这个最大值,若不存在,请说明理由.
的面积有最大值,若存在,求出这个最大值,若不存在,请说明理由.

【答案】(1)![]() ;(2)
;(2)![]() (3)存在,
(3)存在,![]() (m为点P的横坐标)当m=
(m为点P的横坐标)当m=![]() 时,
时,![]()
![]()
【解析】
(1)把A、B坐标代入二次函数解析式,求出a、b,即可求得解析式;
(2)根据第(1)问求出的函数解析式可得出C点的坐标,根据C、P两点横坐标一样可得出P点的坐标,将△BCE的面积分成△PCE与△PCB,以PC为底,即可求出△BCE的面积.
(3)设动点P的坐标为(m,m+2),点C的坐标为(m,![]() ),表示出PC的长度,根据
),表示出PC的长度,根据![]() ,构造二次函数,然后求出二次函数的最大值,并求出此时m的值即可.
,构造二次函数,然后求出二次函数的最大值,并求出此时m的值即可.
解:(1)∵A(![]() )和B(4,6)在抛物线y=ax2+bx+6上,
)和B(4,6)在抛物线y=ax2+bx+6上,
∴
解得:![]() ,
,
∴抛物线的解析式![]() ;
;
(2)∵二次函数解析式为![]() ,
,
∴顶点C坐标为![]() ,
,
∵PC⊥x,点P在直线y=x+2上,
∴点P的坐标为![]() ,
,
∴PC=6;
∵点E为直线y=x+2与x轴的交点,
∴点E的坐标为![]()
∵ ![]() =
=![]()
∴![]() .
.
(3)存在.
设动点P的坐标是![]() ,点C的坐标为
,点C的坐标为![]() ,
,
∵![]()
![]()
∴![]()
∵![]() ,
,
∴函数开口向下,有最大值
∴当![]() 时,△ABC的面积有最大值为
时,△ABC的面积有最大值为![]() .
.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月
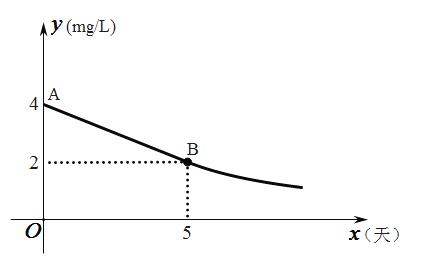
月![]() 日贵州环保行活动“美丽乌江 拒绝污染”正式开启,乌江支流由于长期采磷及磷化工发展造成了总磷污染.当地政府提出五条整改措施,力求在
日贵州环保行活动“美丽乌江 拒绝污染”正式开启,乌江支流由于长期采磷及磷化工发展造成了总磷污染.当地政府提出五条整改措施,力求在![]() 天以内使总磷含量达标(即总磷浓度低于
天以内使总磷含量达标(即总磷浓度低于![]() ).整改过程中,总磷浓度
).整改过程中,总磷浓度![]() 与时间
与时间![]() (天)的变化规律如图所示,其中线段
(天)的变化规律如图所示,其中线段![]() 表示前
表示前![]() 天的变化规律,且线段
天的变化规律,且线段![]() 所在直线的表达式为:
所在直线的表达式为:![]() ,从第
,从第![]() 天起,该支流总磷浓度
天起,该支流总磷浓度![]() 与时间
与时间![]() 成反比例关系.
成反比例关系.
(1)求整改全过程中总磷浓度![]() 与时间
与时间![]() 的函数表达式;
的函数表达式;
(2)该支流中总磷的浓度能否在![]() 天以内达标?说明理由.
天以内达标?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以矩形ABCD的边CD为直径作⊙O,点E是AB 的中点,连接CE交⊙O于点F,连接AF并延长交BC于点H.

(1)若连接AO,试判断四边形AECO的形状,并说明理由;
(2)求证:AH是⊙O的切线;
(3)若AB=6,CH=2,则AH的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
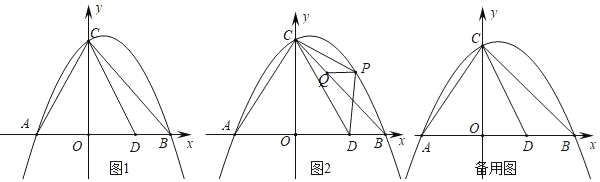
【题目】如图1,抛物线与y=﹣![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC,点D是线段AB上一点,且AD=CA,连接CD.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC,点D是线段AB上一点,且AD=CA,连接CD.
(1)如图2,点P是直线BC上方抛物线上的一动点,在线段BC上有一动点Q,连接PC、PD、PQ,当△PCD面积最大时,求PQ+![]() CQ的最小值;
CQ的最小值;
(2)将过点D的直线绕点D旋转,设旋转中的直线l分别与直线AC、直线CO交于点M、N,当△CMN为等腰三角形时,直接写出CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商销售每箱进价为40元的柑橘,物价部门规定每箱售价不得高于55元;市场调查发现,若每箱以45元的价格销售,平均每天销售105箱;每箱以50元的价格销售,平均每天销售90箱.假定每天销售量y(箱)与销售价x(元/箱)之间满足一次函数关系式.
(1)求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式;
(2)求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式;
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
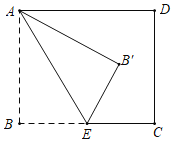
【题目】如图,在矩形ABCD中,已知AB=2,点E是BC边的中点,连接AE,△AB′E和△ABE关于AE所在直线对称,若△B′CD是直角三角形,则BC边的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com