练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知和，点在边上，，边与相交于点．

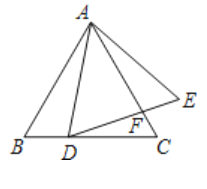
    （1）求证：；

    （2）如果，求证：．

    【答案】（1）见解析；（2）见解析

    【解析】

    （1）根据等边对等角得到，通过证明△ABC∽△FDA得对应边成比例，化比例式为等积式即可；

    （2）通过证明△AEF∽△CDF和△ABD∽△EDA,根据相似三角形的性质列两个比例式，用等量代换即可得.

    （1）证明：∵AD=DC,

    ∴∠DAC=∠C,

    ∵∠ADE=∠B,

    ∴△ABC∽△FDA,

    ∴ ,

    ∴.

    （2）证明：∵AE∥BC,

    ∴∠E=∠EDC, ∠EAC=∠C,

    ∴△AEF∽△CDF,

    ∴ ,

    ∴,

    ∵∠ADC=∠ADE+∠EDC=∠B+∠BAD, ∠ADE=∠B,

    ∴∠BAD=∠EDC,

    ∴∠BAD=∠E,

    ∴△ABD∽△EDA,

    ∴ ,

    ∴,

    ∴.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

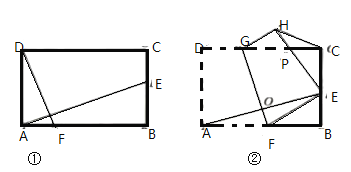
    【题目】（1）如图①，在矩形中，分别是上的点，且，求的值；

    （2）如图②，在矩形中（为常数），将矩形沿折叠，使点落在边上的点处，得到四边形交于点，连接交于点，求的值；

    （3）在（2）的条件下，连接，当时，若，求的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y＝ax2+bx+3经过点A（﹣1，0），B（3，0），与y轴交于点C．点D（xD，yD）为抛物线上一个动点，其中1＜xD＜3．连接AC，BC，DB，DC．

    （1）求该抛物线的解析式；

    （2）当△BCD的面积等于△AOC的面积的2倍时，求点D的坐标；

    （3）在（2）的条件下，若点M是x轴上一动点，点N是抛物线上一动点，试判断是否存在这样的点M，使得以点B，D，M，N为顶点的四边形是平行四边形．若存在，求出点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某品牌牛奶供应商提供A，B，C，D四种不同口味的牛奶供学生饮用．某校为了了解学生对不同口味的牛奶的喜好，对全校订牛奶的学生进行了随机调查，并根据调查结果绘制了如下两幅不完整的统计图．根据统计图的信息解决下列问题：

    （1）本次调查的学生有多少人？

    （2）补全上面的条形统计图；

    （3）扇形统计图中C对应的中心角度数是_____；

    （4）若该校有600名学生订了该品牌的牛奶，每名学生每天只订一盒牛奶，要使学生能喝到自己喜欢的牛奶，则该牛奶供应商送往该校的牛奶中，A，B口味的牛奶共约多少盒？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

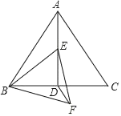
    【题目】如图，在边长为2的等边△ABC中，D是BC的中点，点E在线段AD上，连结BE，在BE的下方作等边△BEF，连结DF．当△BDF的周长最小时，∠DBF的度数是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y=x+2与抛物线y=ax2+bx+6（a≠0）相交于A（）和B（4，6），点P是线段AB上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．

    （1）求抛物线的解析式；

    （2）当C为抛物线顶点的时候，求的面积.

    （3）是否存在质疑的点P，使的面积有最大值，若存在，求出这个最大值，若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

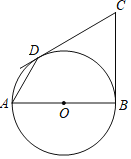
    【题目】如图，AB是⊙O直径，BC⊥AB于点B，点C是射线BC上任意一点，过点C作CD切⊙O于点D，连接AD．

    (1)求证：BC＝CD；

    (2)若∠C＝60°，BC＝3，求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y＝ax2+bx+c中，函数y与自变量x的部分对应值如表：

    x

    …

    ﹣1

    0

    1

    2

    4

    …

    y

    …

    10

    1

    ﹣2

    1

    25

    …

    （1）求这个二次函数的解析式；

    （2）写出这个二次函数图象的开口方向、对称轴和顶点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】9月、10月是房地产行业的传统销售旺季，素来有“金九银十”之称，重庆某开发商两江新区项目部为了赶上销售旺季，在今年9月推出小高层和洋房两种房型共100套，其中洋房每价格是小高层每套价格的2倍．

    （1）该项目部9月份推出的两种房型全部售完，其中小高层销售额为7200万元，洋房销售额为9600万元，则小高层每套价格为多少万元？

    （2）国家明确表态：“坚持房子是用来住的，不是用来炒的，落实房地产长效管理机制，不将房地产作为短期刺激经济的手段．”随后出台“银行资金不得流向房市”等相关政策．受政策及经济大环境影响，市民购房欲望下降，房市遇冷，在（1）问的基础上，10月份小高层每套降价a%，洋房每套降价2a%：为完成10月份销售任务，该项目部决定小高层的套数增加a%，洋房的套数增加%；到月底，小高层卖出95%，洋房卖出80%；为回笼资金，该项目部在该月最后一天推出6套“钜惠”商铺，每套380万元，且成功将6套商铺全部售出，最终实现10月份总销售额在9月份总销售额基础上增加a%，求a的值．

    查看答案和解析>>

    同步练习册答案