
【题目】如图1,在长方形ABCD中,AB=12cm,BC=10cm,点P从A出发,沿A→B→C→D的路线运动,到D停止;点Q从D点出发,沿D→C→B→A路线运动,到A点停止.若P、Q两点同时出发,速度分别为每秒lcm、2cm,a秒时P、Q两点同时改变速度,分别变为每秒2cm、![]() cm(P、Q两点速度改变后一直保持此速度,直到停止),如图2是△APD的面积s(cm2)和运动时间x(秒)的图象.
cm(P、Q两点速度改变后一直保持此速度,直到停止),如图2是△APD的面积s(cm2)和运动时间x(秒)的图象.
(1)求出a值;
(2)设点P已行的路程为y1(cm),点Q还剩的路程为y2(cm),请分别求出改变速度后,y1、y2和运动时间x(秒)的关系式;
(3)求P、Q两点都在BC边上,x为何值时P、Q两点相距3cm?

【答案】(1)6;(2)10或![]() ;
;
【解析】
(1)根据图象变化确定a秒时,P点位置,利用面积求a;
(2)P、Q两点的函数关系式都是在运动6秒的基础上得到的,因此注意在总时间内减去6秒;
(3)以(2)为基础可知,两个点相距3cm分为相遇前相距或相遇后相距,因此由(2)可列方程.
(1)由图象可知,当点P在BC上运动时,△APD的面积保持不变,则a秒时,点P在AB上.
![]() ,
,
∴AP=6,
则a=6;
(2)由(1)6秒后点P变速,则点P已行的路程为y1=6+2(x﹣6)=2x﹣6,
∵Q点路程总长为34cm,第6秒时已经走12cm,
故点Q还剩的路程为y2=34﹣12﹣![]() ;
;
(3)当P、Q两点相遇前相距3cm时,
![]() ﹣(2x﹣6)=3,解得x=10,
﹣(2x﹣6)=3,解得x=10,
当P、Q两点相遇后相距3cm时,
(2x﹣6)﹣(![]() )=3,解得x=
)=3,解得x=![]() ,
,
∴当x=10或![]() 时,P、Q两点相距3cm
时,P、Q两点相距3cm


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标为(﹣1,1),点B在x轴正半轴上,点D在第三象限的双曲线y=![]() 上,过点C作CE∥x轴交双曲线于点E,则CE的长为( )
上,过点C作CE∥x轴交双曲线于点E,则CE的长为( )

A. ![]() B.
B. ![]() C. 3.5D. 5
C. 3.5D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下面的解题过程的横线上填空,并在括号内注明理由。
如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.

解:∵∠A=∠F(已知)
∴DF∥AC(_____________________)
∴∠D=_____(______________________)
∵∠C=∠D(已知)
∴∠1=_____(___________________)
∴BD∥CE(_______________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实际问题
某批发商以![]() 元/
元/ ![]() 的成本价购入了某产品
的成本价购入了某产品![]() ,据市场预测,该产品的销售价
,据市场预测,该产品的销售价![]() (元/
(元/ ![]() )与保存时间
)与保存时间![]() (天)的函数关系为
(天)的函数关系为![]() ,但保存这批产品平均每天将损耗
,但保存这批产品平均每天将损耗![]() .另外,批发商每天保存该批产品的费用为
.另外,批发商每天保存该批产品的费用为![]() 元.已知该产品每天的销量不超过
元.已知该产品每天的销量不超过![]() ,若批发商希望通过这批产品卖出获利
,若批发商希望通过这批产品卖出获利![]() 元,则批发商应在保存该产品多少天时一次性卖出?
元,则批发商应在保存该产品多少天时一次性卖出?
小明的思路及解答
本题的相等关系是:
销售价![]() 销量
销量![]() 成本价
成本价![]() 销量
销量![]() 保存费用
保存费用![]() 获利.
获利.
解:设批发商应在保存该产品![]() 天时一次性卖出可获利
天时一次性卖出可获利![]() 元.
元.
根据上面的相等关系,
得![]() .
.
解这个方程,得![]() ,
, ![]() .
.
当![]() 时,
时, ![]() (不合题意,舍去),
(不合题意,舍去),
当![]() 时,
时, ![]() .
.
答:批发商应在保存该产品![]() 天时一次性卖出可获利
天时一次性卖出可获利![]() 元.
元.
数学老师的批改
数学老师在小明的解答中画了一条横线,并打了一个“![]() ”.
”.
你的观点及做法
(![]() )请指出小明错误的原因.
)请指出小明错误的原因.
(![]() )重新给出正确的解答过程.
)重新给出正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 分别为
分别为![]() 边上的动点.
边上的动点.
(1)若点![]() 分别为
分别为![]() 的中点,求线段
的中点,求线段![]() 的长;
的长;
(2)若![]() ,
,
①求证: ![]() ∽
∽![]() ;
;
②试问![]() 与
与![]() 相似吗?并说明理由.
相似吗?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2),
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2),
(1)求这两个函数的关系式;
(2)观察图象,写出使得y1>y2成立的自变量x的取值范围;
(3)如果点C与点A关于x轴对称,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为( )
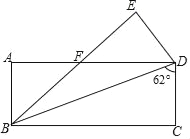
A. 31° B. 28° C. 62° D. 56°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,分别探索下列四个图形中∠P、∠A、∠C,发现有如下三种数量关系:∠A+∠C =∠P ;∠P+∠A =∠C ;∠P+∠C =∠A,请你选择其中的两种数量关系说明理由.
(1)我选择的是图 ,数量关系式是 .
理由:
(2) 我选择的是图 ,数量关系式是 .
理由:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com