
【题目】已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,AE⊥BD垂足为E.
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.
【答案】
(1)证明:∵AB=AD=25,
∴∠ABD=∠ADB,
∵AD∥BC,
∴∠ADB=∠DBC,
∴∠ABD=∠DBC,
∵AE⊥BD,
∴∠AEB=∠C=90°,
∴△ABE∽△DBC
(2)解:∵AB=AD,又AE⊥BD,
∴BE=DE,
∴BD=2BE,
由△ABE∽△DBC,
得 ![]() ,
,
∵AB=AD=25,BC=32,
∴ ![]() ,
,
∴BE=20,
∴AE= ![]() .
.
【解析】(1)利用平行线和等腰三角形性质可推出两角对应相等,进而推出两三角形相似;(2)由三角形相似△ABE∽△DBC推出对应边成比例先求BE,再利用勾股定理求出AE.
【考点精析】利用勾股定理的概念和直角梯形对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;一腰垂直于底的梯形是直角梯形.


科目:初中数学 来源: 题型:
【题目】密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物,是美国最高的独自挺立的纪念碑,如图.拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度.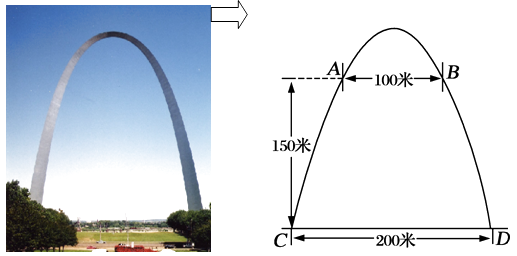
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形纸片ABCD的边长为3,点E,F分别在边BC、CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( )
A.1.5
B.2.5
C.2.25
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支援雅安灾区,某学校计划用“义捐义卖”活动中筹集的部分资金用于购买A,B两种型号的学习用品共1000件,已知A型学习用品的单价为20元,B型学习用品的单价为30元.
(1)若购买这批学习用品用了26000元,则购买A,B两种学习用品各多少件?
(2)若购买这批学习用品的钱不超过28000元,则最多购买B型学习用品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在《几何原本》中记载着这样的题目:如果同一条线段被两个分点先后分成相等和不相等的线段,以得到的各线段为边作正方形,那么不相等的两个正方形的面积之和等于原线段一半上的正方形与两个分点之间一段上正方形的面积之和的两倍.王老师带领学生在阅读的基础上画出的部分图形如图,已知线段![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 上任意一点(
上任意一点(![]() 不与
不与![]() 重合),分别以
重合),分别以![]() 和
和![]() 为边在
为边在![]() 的下方作正方形
的下方作正方形![]() 和正方形
和正方形![]() ,以
,以![]() 和
和![]() 为边在线段下方作正方形
为边在线段下方作正方形![]() 和正方形
和正方形![]() ,则正方形
,则正方形![]() 与正方形
与正方形![]() 的面积之和等于正方形
的面积之和等于正方形![]() 和正方形
和正方形![]() 面积之和的两倍.
面积之和的两倍.
(1)请你画出正方形![]() 和正方形
和正方形![]() (不必尺规作图);
(不必尺规作图);
(2)设![]() ,
,![]() ,根据题意写出关于
,根据题意写出关于![]() 的等式并证明.
的等式并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=4,BC=2,点D是边AB上一点,CD将△ABC分成△ACD和△BCD,若△ACD是以AC为底的等腰三角形,且△BCD与△BAC相似,则CD的长为( )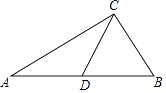
A.![]()
B.2
C.4 ![]() ﹣4
﹣4
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M,N是边AD上的两点,连接MO,NO,并分别延长交边BC于两点M′,N′,则图中的全等三角形共有( )
A.2对
B.3对
C.4对
D.5对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)已知,在平面直角坐标系中,AB⊥x轴于点B,点A(a,b)满足![]() +|b-2|=0,平移线段AB使点A与原点重合,点B的对应点为点C.
+|b-2|=0,平移线段AB使点A与原点重合,点B的对应点为点C.
(1)则a=____,b=____;点C坐标为________;
(2)如下图所示:点D(m, n)在线段BC上,求m、n满足的关系式;

(3)如下图所示:E是线段OB上一动点,以OB为边作∠G=∠AOB,,交BC于点G,连CE交OG于点F,的当点E在线段OB上运动过程中, ![]() 的值是否会发生变化?若变化请说明理由,若不变,请求出其值.
的值是否会发生变化?若变化请说明理由,若不变,请求出其值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com