
����Ŀ��(12��)��֪����ƽ��ֱ������ϵ��,AB��x���ڵ�B,��A(a,b)����![]() +|b-2|=0,ƽ���߶�ABʹ��A��ԭ���غ�,��B�Ķ�Ӧ��Ϊ��C.
+|b-2|=0,ƽ���߶�ABʹ��A��ԭ���غ�,��B�Ķ�Ӧ��Ϊ��C.
(1)��a=____,b=____;��C����Ϊ________;
(2)����ͼ��ʾ����D(m, n)���߶�BC��,��m��n����Ĺ�ϵʽ;

(3)����ͼ��ʾ��E���߶�OB��һ����,��OBΪ������G=��AOB,,��BC�ڵ�G����CE��OG�ڵ�F,�ĵ���E���߶�OB���˶�������, ![]() ��ֵ�Ƿ�ᷢ���仯?���仯��˵������,������,�������ֵ.
��ֵ�Ƿ�ᷢ���仯?���仯��˵������,������,�������ֵ.

���𰸡� ��1��4 2 ��0����2������2��m-2n=4;(3)���䣬 ![]() ���ɼ�����.
���ɼ�����.
����������1��a= 4 ��b= 2 ����C��������0��-2����
��2����ͼ1������D�ֱ���DM��x���ڵ�M�� DN��y���ڵ�N������OD��
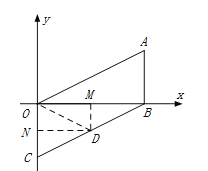
��AB�� x���ڵ�B���ҵ�A��D��C���������ֱ�Ϊ����4��2������m��n������0��-2��
��OB=4��OC=2��MD=-n��ND=m
�� S��BOC=![]()
![]() OB��OC=4
OB��OC=4
�֡�S��BOC = S��BOD��S��COD
=![]() OB��MD��
OB��MD��![]() OC��ND
OC��ND
=![]() ��4����-n��+
��4����-n��+![]() ��m��2
��m��2
=m-2n
��m-2n=4��������(7��)
��3���⣺ ![]()
![]() ��ֵ���䣬ֵΪ2���������£�
��ֵ���䣬ֵΪ2���������£�
��ͼ��ʾ���ֱ����E��F��EP��OA�� FQ��OA�ֱ�y���ڵ�P����Q

���߶�OC�����߶�ABƽ�Ƶõ�
��BC��OA �֡�EP��OA
��EP��BC
���GCF=��PEC
��EP��OA
���AOE=��OEP
���OEC=��OEP+��PEC
=��AOE+��GCF ͬ������OFC=��AOF+��GCF��������(10��)
�֡ߡ�AOB=��BOG
���OFC=2��AOE+��GCF
��![]()
![]()
![]() =2
=2


 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
��ͨ����ͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ֱ������ABCD�У�AD��BC����C=90�㣬AB=AD=25��BC=32������BD��AE��BD����ΪE��
��1����֤����ABE�ס�DBC��
��2�����߶�AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��գ���֪��ͼ��AD��BC��D��EG��BC��G����E=��1��
��֤��ADƽ����BAC��
֤������AD��BC��D��EG��BC��G�� ��֪ ��
���ADC=90�㣬��EGC=90����___________��
���ADC=��EGC������������
��AD��EG��_____________��
���1=��2��___________��
��E=��3��___________��
���ߡ�E=��1�� ��֪��
���2=��3��___________��
��ADƽ����BAC��___________����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߱���ABCDEFG�У�AB��ED���ӳ����ཻ��O�㣮��ͼ�С�1����2����3����4����ǵĽǶȺ�Ϊ220�������BOD�Ķ����ǣ�������

A. 400 B. 450 C. 500 D. 600
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����D�ǡ�ABC����ƽ����һ�㣬����AD��CD��
��1����ͼ1������A��28�㣬��B��72�㣬��C��11�㣬���ADC��
��2����ͼ2��������һ��P��ʹ��PBƽ�֡�ABC��ͬʱPDƽ�֡�ADC��̽����A����P����C�Ĺ�ϵ��֤����
��3����ͼ3���� ��2���������£�����D������ABC���ⲿ�������������䣬̽����A����P����C�Ĺ�ϵ��֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������ͼ��ʾ�Ķ��κ���y=ax2+bx+c��ͼ���У��۲�ó�������������Ϣ����1��a��O����2��b2��4ac��0����3��b��O����4��a+b+c��0����5��a��b+c��0������Ϊ������ȷ��Ϣ�ĸ����У� ��
A.2��
B.3��
C.4��
D.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ����������a��b���ĺ���Ϊ����a��bʱ��a��b=a+b����a��bʱ��a��b=a-b�����磺3�-4��=3+��-4��=-1����-6����![]() =-6-
=-6-![]() =-6
=-6![]() ��
��
��1����գ���-4����3=______��
��2�������3x-4���2x+8��=��3x-4��-��2x+8������x��ȡֵ��Χ��
��3�������3x-7���3-2x��=2����x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���������ܱ�ʾΪ������������ƽ����,������������Ϊ���ǻ���������![]() ,
,![]() ��.��֪�ǻ�������С�����˳���������У�
��.��֪�ǻ�������С�����˳���������У�![]() ���
���![]() ���ǻ�����__________.
���ǻ�����__________.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com