
【题目】若一个正整数能表示为两个正整数的平方差,则称这个正整数为“智慧数”(如![]() ,
,![]() ).已知智慧数按从小到大的顺序构成如下数列:
).已知智慧数按从小到大的顺序构成如下数列:![]() 则第
则第![]() 个智慧数是__________.
个智慧数是__________.
【答案】2695
【解析】
如果一个数是智慧数,就能表示为两个正整数的平方差,设这两个数分别m、n,设m>n,即智慧数=m2-n2=(m+n)(m-n),因为m,n是正整数,因而m+n和m-n就是两个自然数.要判断一个数是否是智慧数,可以把这个数分解因数,分解成两个整数的积,看这两个数能否写成两个正整数的和与差.
解:1不能表示为两个正整数的平方差,所以1不是“智慧数”.对于大于1的奇正整数2k+1,有2k+1=(k+1)2-k2(k=1,2,…).所以大于1的奇正整数都是“智慧数”.
对于被4整除的偶数4k,有4k=(k+1)2-(k-1)2(k=2,3,…).
即大于4的被4整除的数都是“智慧数”,而4不能表示为两个正整数平方差,所以4不是“智慧数”.
对于被4除余2的数4k+2(k=0,1,2,3,…),设4k+2=x2-y2=(x+y)(x-y),其中x,y为正整数,
当x,y奇偶性相同时,(x+y)(x-y)被4整除,而4k+2不被4整除;
当x,y奇偶性相异时,(x+y)(x-y)为奇数,而4k+2为偶数,总得矛盾.
所以不存在自然数x,y使得x2-y2=4k+2.即形如4k+2的数均不为“智慧数”.
因此,在正整数列中前四个正整数只有3为“智慧数”,此后,每连续四个数中有三个“智慧数”.
因为2017=(1+3×672),4×(672+1)=2692,所以2692是第2017个“智慧数”,
所以2693是第2018个“智慧数”,2694÷4=673……2,所以不是智慧数,2695是第2019个“智慧数”,
故答案为: 2695.


科目:初中数学 来源: 题型:
【题目】(12分)已知,在平面直角坐标系中,AB⊥x轴于点B,点A(a,b)满足![]() +|b-2|=0,平移线段AB使点A与原点重合,点B的对应点为点C.
+|b-2|=0,平移线段AB使点A与原点重合,点B的对应点为点C.
(1)则a=____,b=____;点C坐标为________;
(2)如下图所示:点D(m, n)在线段BC上,求m、n满足的关系式;

(3)如下图所示:E是线段OB上一动点,以OB为边作∠G=∠AOB,,交BC于点G,连CE交OG于点F,的当点E在线段OB上运动过程中, ![]() 的值是否会发生变化?若变化请说明理由,若不变,请求出其值.
的值是否会发生变化?若变化请说明理由,若不变,请求出其值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.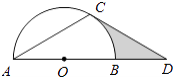
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点分别为A(2,4),B(﹣2,2),C(3,1).
(1)作出△ABC关于x轴对称的图形△DEF,写出顶点D、E、F的坐标.
(2)如果点H(3m﹣1,n﹣6)与点H′(2n+7,3m﹣9)关于y轴对称,求m,n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-6,1),点B的坐标为(-3,1),点C的坐标为(-3,3).将Rt△ABC绕点B顺时针旋转90°得到Rt△A1B1C1 , 试在图上画出的图形Rt△A1B1C1的图形,并写出点A1 , C1的坐标;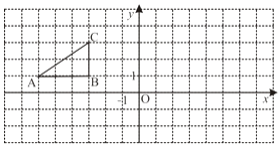
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+b图象经过点(1,3)和(4,6)
①试求![]() 与
与![]() ;
;

②画出这个一次函数图象;
③这个一次函数与y轴交点坐标是( )
④当x 时,y<0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com