Question

【题目】如图，点D在⊙O的直径AB的延长线上，点C在⊙O上，AC=CD，∠ACD=120°．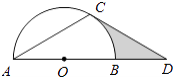

（1）求证：CD是⊙O的切线；
（2）若⊙O的半径为2，求图中阴影部分的面积．

Answer 1

【答案】
（1）证明：连接OC．

∵AC=CD，∠ACD=120°，

∴∠A=∠D=30°．

∵OA=OC，

∴∠2=∠A=30°．

∴∠OCD=180°﹣∠A﹣∠D﹣∠2=90°．即OC⊥CD，

∴CD是⊙O的切线．

（2）解：∵∠A=30°，

∴∠1=2∠A=60°．

∴S扇形BOC= ．

在Rt△OCD中，

∵ = ，

∴ = ．

∴ ．

∴图中阴影部分的面积为： ．

【解析】（1）要证CD是⊙O的切线，点C在半圆上，因此连接OC，需证明OC⊥CD。先根据等腰三角形的性质及三角形内角和定理求出∠2=∠A=∠D=30°．再求出∠OCD的度数，就可证出结论。
（2）根据图形分析阴影部分的面积=Rt△OCD的面积-扇形COB的面积，根据题意易求出∠1的度数，再利用解直角三角形求出CD的长，然后求出Rt△OCD的面积和扇形COB的面积，即可求得结果。