


科目:初中数学 来源: 题型:
 如图,在直角坐标系中直线分别交x轴、y轴于A(4,0)、B(0,-3)两点,现有一半径为1的动圆,圆心位于B点处,沿着BA方向以每秒1个单位的速率做平移运动,则经过
如图,在直角坐标系中直线分别交x轴、y轴于A(4,0)、B(0,-3)两点,现有一半径为1的动圆,圆心位于B点处,沿着BA方向以每秒1个单位的速率做平移运动,则经过查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 冬至时是一年中太阳相对于地球位置最低的时刻,只要此时能采到阳光,一年四季就均能受到阳光照射.此时竖一根a米长的竹杆,其影长为b米,某单位计划想建m米高的南北两幢宿舍楼(如图所示).当两幢楼相距多少米时,后楼的采光一年四季不受影响?( )
冬至时是一年中太阳相对于地球位置最低的时刻,只要此时能采到阳光,一年四季就均能受到阳光照射.此时竖一根a米长的竹杆,其影长为b米,某单位计划想建m米高的南北两幢宿舍楼(如图所示).当两幢楼相距多少米时,后楼的采光一年四季不受影响?( )A、
| ||
B、
| ||
C、
| ||
| D、abm米 |
查看答案和解析>>
科目:初中数学 来源: 题型:
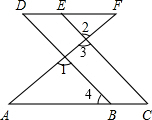 认真阅读并填空
认真阅读并填空查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com