
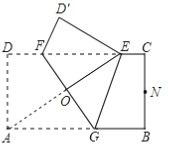
【题目】如图,矩形纸片ABCD中,AD=1,AB=2.将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB、CD交于点G、F,AE与FG交于点O.当△AED的外接圆与BC相切于BC的中点N.则折痕FG的长为______.
【答案】![]()
【解析】试题分析:设AE与FG的交点为O. 根据轴对称的性质,得AO=EO.
取AD的中点M,连接MO. 则MO=![]() DE,MO∥DC.
DE,MO∥DC.
设DE=x,则MO=![]() x, 在矩形ABCD中,∠C=∠D=90°,
x, 在矩形ABCD中,∠C=∠D=90°,
所以AE为△AED的外接圆的直径,O为圆心. 延长MO交BC于点N,则ON∥CD.
所以∠CNM=180°-∠C=90°. 所以ON⊥BC,四边形MNCD是矩形.
所以MN=CD=AB=2.所以ON=MN-MO=2-![]() x.
x.
因为△AED的外接圆与BC相切, 所以ON是△AED的外接圆的半径.
所以OE=ON=2-![]() x,AE=2ON=4-x.
x,AE=2ON=4-x.
根据Rt△AED的勾股定理可得:x=![]() 所以DE=
所以DE=![]() ,OE=2-
,OE=2-![]() x=
x=![]() .
.
根据轴对称的性质,得AE⊥FG. 所以∠FOE=∠D=90°.可得FO=![]() .
.
又AB∥CD,所以∠EFO=∠AGO,∠FEO=∠GAO. 所以△FEO≌△GAO.所以FO=GO.
所以FG=2FO=![]() 所以折痕FG的长是
所以折痕FG的长是![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(1,2),B(3,1),C(﹣2,﹣1). 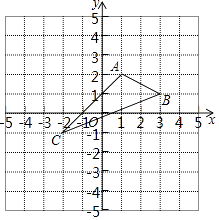
(1)在图中作出△ABC关于x轴的对称图形△A1B1C1 .
(2)写出点A1 , B1 , C1的坐标(直接写答案)
A1
B1
C1
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=4cm,AB=7cm,AD平分∠BAC交BC于点D,DE⊥AB于点E,则EB的长是( ) 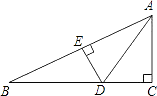
A.3 cm
B.4 cm
C.5 cm
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
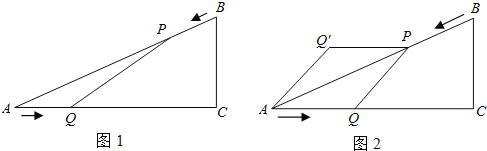
【题目】如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6 cm ,如果点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm /s,连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
(1)当t为何值时,PQ∥BC.
(2)是否存在某时刻t,使线段PQ恰好把△ABC的面积平分?若存在求出此时t的值;若不存在,请说明理由.
(3)如图2,把△APQ沿AP翻折,得到四边形AQPQ′.那么是否存在某时刻t使四边形AQPQ′为菱形?若存在,求出此时菱形的面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AE⊥BC于E,AE=BE,D是AE上的一点,且DE=CE,连接BD,CD.
(1)试判断BD与AC的位置关系和数量关系,并说明理由;
(2)如图2,若将△DCE绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
(3)如图3,若将(2)中的等腰直角三角形都换成等边三角形,其他条件不变.
①试猜想BD与AC的数量关系,并说明理由;
②你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把两根钢条AA′,BB′的中点O连在一起,可以做成一个测量工件内槽宽的工具(工人把这种工具叫卡钳)只要量出A′B′的长度,就可以知道工件的内径AB是否符合标准,你能简要说出工人这样测量的道理吗?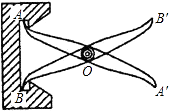
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是必然事件的是( )
A.明天太阳从西方升起
B.打开电视机,正在播放广告
C.掷一枚硬币,正面朝上
D.任意一个三角形,它的内角和等于180°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com