
����Ŀ����ͼ1���ڡ�ABC�У�AE��BC��E��AE=BE��D��AE�ϵ�һ�㣬��DE=CE������BD��CD��
��1�����ж�BD��AC��λ�ù�ϵ��������ϵ����˵�����ɣ�
��2����ͼ2��������DCE�Ƶ�E��תһ���ĽǶȺ����ж�BD��AC��λ�ù�ϵ��������ϵ�Ƿ����仯����˵�����ɣ�
��3����ͼ3��������2���еĵ���ֱ�������ζ����ɵȱ������Σ������������䣮
���Բ���BD��AC��������ϵ����˵�����ɣ�
���������BD��AC�ļнǶ���������ܣ���ֱ��д���нǶ�����������ܣ���˵�����ɣ�
���𰸡�
��1��
�⣺BD=AC��BD��AC��
���ɣ��ӳ�BD��AC��F��
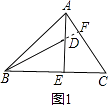
��AE��BC��
���AEB=��AEC=90�㣬
�ڡ�BED�͡�AEC�� 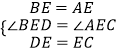
���BED�ա�AEC��
��BD=AC����DBE=��CAE��
�ߡ�BED=90�㣬
���EBD+��BDE=90�㣬
�ߡ�BDE=��ADF��
���ADF+��CAE=90�㣬
���AFD=180�㩁90��=90�㣬
��BD��AC
��2��
�⣺
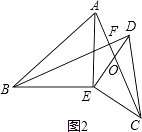
�������仯��
�����ǣ��ߡ�BEA=��DEC=90�㣬
���BEA+��AED=��DEC+��AED��
���BED=��AEC��
�ڡ�BED�͡�AEC�� 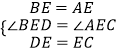
���BED�ա�AEC��
��BD=AC����BDE=��ACE��
�ߡ�DEC=90�㣬
���ACE+��EOC=90�㣬
�ߡ�EOC=��DOF��
���BDE+��DOF=90�㣬
���DFO=180�㩁90��=90�㣬
��BD��AC
��3��
�⣺�ܣ�
���ɣ��ߡ�ABE�͡�DEC�ǵȱ������Σ�
��AE=BE��DE=EC����EDC=��DCE=60�㣬��BEA=��DEC=60�㣬
���BEA+��AED=��DEC+��AED��
���BED=��AEC��
�ڡ�BED�͡�AEC���� 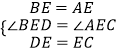
���BED�ա�AEC��
���BDE=��ACE��
���DFC=180�㩁����BDE+��EDC+��DCF��
=180�㩁����ACE+��EDC+��DCF��
=180�㩁��60��+60�㣩
=60�㣬
��BD��AC���ɵĽǵĶ���Ϊ60���120��
����������1���ӳ�BD��AC��F�������AEB=��AEC=90�㣬֤����BED�ա�AEC���Ƴ�BD=AC����DBE=��CAE�����ݡ�EBD+��BDE=90���Ƴ���ADF+��CAE=90�㣬�����AFD=90�㼴�ɣ���2�������BED=��AEC��֤����BED�ա�AEC���Ƴ�BD=AC����BDE=��ACE�����ݡ�ACE+��EOC=90�������BDE+��DOF=90�㣬�����DFO=90�㼴�ɣ���3�������BED=��AEC��֤����BED�ա�AEC���Ƴ���BDE=��ACE�������������ڽǺͶ��������DFC���ɣ�
�����㾫�������������ε��ڽǺ���Ǻ�ȫ�������ε������ǽ����ĸ�������Ҫ֪�������ε������ڽ��У�ֻ������һ���ڽ���ֱ�ǻ�۽ǣ�ֱ�������ε�������ǻ��ࣻ�����ε�һ����ǵ��ں��������ڵ������ڽǵĺͣ������ε�һ����Ǵ����κ�һ�����������ڵ��ڽǣ�ȫ�������εĶ�Ӧ�����; ȫ�������εĶ�Ӧ����ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A�ص�B�صĹ�·�辭��C�أ�ͼ��AC=10ǧ�ף���CAB=25�㣬��CBA=37��. ����й滮����Ҫ������A��B����֮����һ����ֱ�Ĺ�·.
��1�����ֱ��Ĺ�·AB�ij���
��2���ʹ�·��ֱ��ö�·�̱�ԭ�������˶���ǧ�ף���sin25���0.42��cos25���0.91,sin37���0.60��tan37���0.75��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ѽ���ͼ��ƴ��һ���µ�ͼ�Σ���ͨ��ͼ������ļ��㣬�������Եõ�һЩ���õ�ʽ�ӣ���������һЩ������ͼ�ε������ 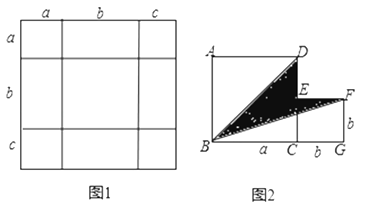
��1����ͼ1���ǽ�����������ȵ�С��������С������ƴ��һ���߳�Ϊa+b+c�������Σ����ò�ͬ�ķ����������ͼ�ε���������ܷ���ʲô���ۣ���д������
��2����ͼ2���ǽ������߳��ֱ�Ϊa��b��������ƴ��һ��B��C��G������ͬһֱ���ϣ�����BD��BF�����������εı߳�����a+b=10��ab=20�����������Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ڡ�ABC�У���A=90�㣬BD�ǡ�ABC��ƽ���ߣ�DE��BC�Ĵ�ֱƽ���ߣ����C= �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽƬABCD�У�AD=1��AB=2����ֽƬ�۵���ʹ����A���CD�ϵĵ�E�غϣ��ۺ�FG�ֱ���AB��CD���ڵ�G��F��AE��FG���ڵ�O������AED�����Բ��BC������BC���е�N�����ۺ�FG�ij�Ϊ______��
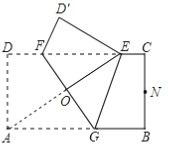
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ͼ����գ�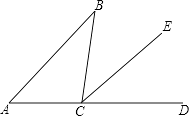
��1����A����ͬλ�ǣ�
��2����B�����ڴ��ǣ�
��3����A����ͬ���ڽǣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪EΪ������ABC�ĵױ�BC��һ���㣬��E��EF��BC��AB��D����CA���ӳ�����F���ʣ� 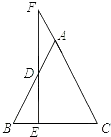
��1����F���ADF�Ĺ�ϵ������˵�����ɣ�
��2����E��BC�ӳ����ϣ������������䣬����Ľ����Ƿ����������������˵�����ɣ�������������ͼ�β�����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
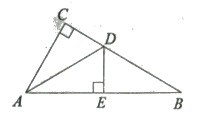
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬ADƽ�֡�CAB,��CB�ڵ�D,DE��AB�ڵ�E.
(1)��֤����ACD�ա�AED
(2)��AC=5����DEB���ܳ�Ϊ8�����ABC���ܳ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com