
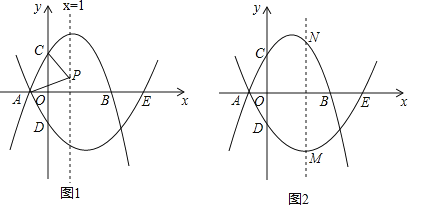
����Ŀ����֪��������l1��y=��x2+bx+3��x���ڵ�A��B������A�ڵ�B����ࣩ����y���ڵ�C����Գ���Ϊx=1��������l2������A����x�����һ������ΪE��5��0������y���ڵ�D��0���� ![]() ����
����
��1����������l2�ĺ�������ʽ��
��2��PΪֱ��x=1��һ���㣬����PA��PC����PA=PCʱ�����P�����ꣻ
��3��MΪ������l2��һ���㣬����M��ֱ��MN��y�ᣬ��������l1�ڵ�N�����M�Ե�A�˶�����E�Ĺ����У��߶�MN���ȵ����ֵ��
���𰸡���1��y=![]() x2��2x��
x2��2x��![]() ����2����1��1������3��12��
����2����1��1������3��12��
�������������������1���ɶԳ�������b�������l1�Ľ���ʽ����y=0�����A�����꣬�����ô���ϵ���������l2�ı���ʽ����2����P������Ϊ��1��y�����ɹ��ɶ����ɱ�ʾ��PC2��PA2���������ɵõ�����y�ķ��̿����y�������P�����ꣻ��3���ɷֱ����M��N�����꣬�ɱ�ʾ��MN���ٸ��ݺ��������ʿ����MN�����ֵ��
�����������1����������l1��y=��x2+bx+3�ĶԳ���Ϊx=1�� �ੁ![]() =1�����b=2��
=1�����b=2��
��������l1�Ľ���ʽΪy=��x2+2x+3�� ��y=0���ɵ���x2+2x+3=0�����x=��1��x=3��
��A����������1��0����
��������l2������A��E���㣬 ������������l2����ʽΪy=a��x+1����x��5����
����������l2��y���ڵ�D��0����![]() ���� �ੁ
���� �ੁ![]() =��5a�����a=
=��5a�����a=![]() �� ��y=
�� ��y=![]() ��x+1����x��5��=
��x+1����x��5��=![]() x2��2x��
x2��2x��![]() ��
��
��������l2�ĺ�������ʽΪy=![]() x2��2x��
x2��2x��![]() ��
��
��2����P������Ϊ��1��y�����ɣ�1���ɵ�C������Ϊ��0��3����
��PC2=12+��y��3��2=y2��6y+10��PA2=[1������1��]2+y2=y2+4�� ��PC=PA��
��y2��6y+10=y2+4�����y=1�� ��P��������1��1����
��3�����������M��x��![]() x2��2x��
x2��2x��![]() ���� ��MN��y�ᣬ ��N��x����x2+2x+3����
���� ��MN��y�ᣬ ��N��x����x2+2x+3����![]() x2��2x��
x2��2x��![]()
����x2+2x+3=![]() x2��2x��
x2��2x��![]() ���ɽ��x=��1��x=
���ɽ��x=��1��x=![]() ��
��
������1��x��![]() ʱ��MN=����x2+2x+3������
ʱ��MN=����x2+2x+3������![]() x2��2x��
x2��2x��![]() ��=��
��=��![]() x2+4x+
x2+4x+![]() =��
=��![]() ��x��
��x��![]() ��2+
��2+![]() ��
��
��Ȼ��1��![]() ��
��![]() ������x=
������x=![]() ʱ��MN�����ֵ
ʱ��MN�����ֵ![]() ��
��
����![]() ��x��5ʱ��MN=��
��x��5ʱ��MN=��![]() x2��2x��
x2��2x��![]() ��������x2+2x+3��=
��������x2+2x+3��=![]() x2��4x��
x2��4x��![]() =
=![]() ��x��
��x��![]() ��2��
��2��![]() ��
��
��Ȼ��x��![]() ʱ��MN��x�����������
ʱ��MN��x�����������
����x=5ʱ��MN�����ֵ��![]() ����5��
����5��![]() ��2��
��2��![]() =12��
=12��
���Ͽ�֪�ڵ�M�Ե�A�˶�����E�Ĺ����У��߶�MN���ȵ����ֵΪ12��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ�����������ε�һ����Ϊ30������������εĶ���Ϊ�� ��
A.120B.30C.120��30D.90
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10��10�������У�ÿ��С�����DZ߳�Ϊ1��С�����Σ�ÿ��С�����εĶ����Ϊ��㣮�������߾���ͼ�е�������㣬�������������Ϊ����������γ�Ϊ�����ߵ����ڽӸ��������������OΪ����ԭ�㽨����ͼ��ʾ��ƽ��ֱ������ϵ����������������Խ���OB����������֮��ľ���Ϊ![]() ���������������������ߵĶ����������ߵ��ڽӸ�������ε��������㣬���������������ҶԳ���ƽ����y��������������ǣ�������
���������������������ߵĶ����������ߵ��ڽӸ�������ε��������㣬���������������ҶԳ���ƽ����y��������������ǣ�������
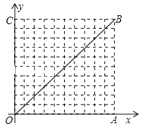
A. 16 B. 15 C. 14 D. 13
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꼶һ��������ͬѧ��һ����ѧ�����еijɼ�ͳ��������±���
�༶ | �μ����� | ��λ�� | ƽ���� | ���� |
һ | 49 | 84 | 80 | 186 |
�� | 49 | 85 | 80 | 161 |
ijͬѧ������õ����½��ۣ�
��һ�������ѧ��ƽ���ɼ���ͬ;
�ڶ���������������һ�ࣨ������85�֣�
��һ��ѧ���ijɼ�����ȶ���������ȷ���ǣ� ��
A. �٢� B. �٢� C. �٢ڢ� D. �ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ͬѧҪ֤������������Ա߷ֱ���ȵ��ı�����ƽ���ı���������ȷ�ģ������ó߹���������ͼ11���ı���ABCD����д�������²���������֪����֤��
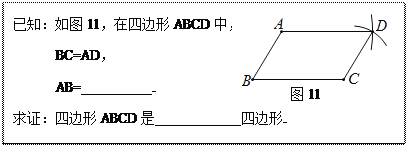

(1)�ڷ�������գ��Բ�ȫ��֪����֤��
(2)�����ͬѧ���뷨д��֤����
֤����
(3)������������֤�����������Ϊ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������в�����ֱ��ԼΪ0.000000085m��0.000000085�ÿ�ѧ��������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������ε������߳��ֱ���7��3���������ĸ�������Ϊ�������߳����ǣ�������
A. 3 B. 4 C. 7 D. 7��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y=ax+b����κ���y=ax2+bx+c��ͬһ����ϵ�е�ͼ������� �� ��
A.  B.
B. 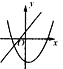 C.
C. 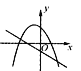 D.
D. 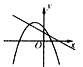
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��˫����y=![]() ��x��0���ϵ�һ���㣬��A��AC��y�ᣬ����Ϊ��C����AC�Ĵ�ֱƽ���߽�˫�����ڵ�B����x���ڵ�D������A��˫�����ϴ������˶�ʱ�����ı���ABCD������ı仯�����С���о������ֿ��ܣ�
��x��0���ϵ�һ���㣬��A��AC��y�ᣬ����Ϊ��C����AC�Ĵ�ֱƽ���߽�˫�����ڵ�B����x���ڵ�D������A��˫�����ϴ������˶�ʱ�����ı���ABCD������ı仯�����С���о������ֿ��ܣ�

������
���ɴ��С����С���
����С������ɴ��С��
�ܲ��䣮
����Ϊ��ȷ����_____��������ţ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com