
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() :
:![]() 相交于
相交于![]() 和点
和点![]() 两点.
两点.
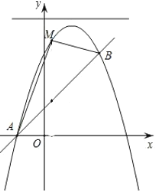
⑴求抛物线![]() 的函数表达式;
的函数表达式;
⑵若点![]() 是位于直线
是位于直线![]() 上方抛物线上的一动点,以
上方抛物线上的一动点,以![]() 为相邻两边作平行四边形
为相邻两边作平行四边形![]() ,当平行四边形
,当平行四边形![]() 的面积最大时,求此时四边形
的面积最大时,求此时四边形![]() 的面积
的面积![]() 及点
及点![]() 的坐标;
的坐标;
⑶在抛物线![]() 的对称轴上是否存在定点
的对称轴上是否存在定点![]() ,使抛物线
,使抛物线![]() 上任意一点
上任意一点![]() 到点
到点![]() 的距离等于到直线
的距离等于到直线![]() 的距离,若存在,求出定点
的距离,若存在,求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】⑴![]() ;⑵当
;⑵当![]() ,
,![]() □MANB=
□MANB=![]() △
△![]() =
=![]() ,此时
,此时![]() ;⑶存在. 当
;⑶存在. 当![]() 时,无论
时,无论![]() 取任何实数,均有
取任何实数,均有![]() . 理由见解析.
. 理由见解析.
【解析】
(1)利用待定系数法,将A,B的坐标代入y=ax2+2x+c即可求得二次函数的解析式;
(2)过点M作MH⊥x轴于H,交直线AB于K,求出直线AB的解析式,设点M(a,-a2+2a+3),则K(a,a+1),利用函数思想求出MK的最大值,再求出△AMB面积的最大值,可推出此时平行四边形MANB的面积S及点M的坐标;
(3)如图2,分别过点B,C作直线y=![]() 的垂线,垂足为N,H,设抛物线对称轴上存在点F,使抛物线C上任意一点P到点F的距离等于到直线y=
的垂线,垂足为N,H,设抛物线对称轴上存在点F,使抛物线C上任意一点P到点F的距离等于到直线y=![]() 的距离,其中F(1,a),连接BF,CF,则可根据BF=BN,CF=CN两组等量关系列出关于a的方程组,解方程组即可.
的距离,其中F(1,a),连接BF,CF,则可根据BF=BN,CF=CN两组等量关系列出关于a的方程组,解方程组即可.
(1)由题意把点(-1,0)、(2,3)代入y=ax2+2x+c,
得,![]() ,
,
解得a=-1,c=3,
∴此抛物线C函数表达式为:y=-x2+2x+3;
(2)如图1,过点M作MH⊥x轴于H,交直线AB于K,
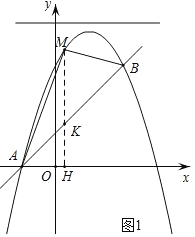
将点(-1,0)、(2,3)代入y=kx+b中,
得,![]() ,
,
解得,k=1,b=1,
∴yAB=x+1,
设点M(a,-a2+2a+3),则K(a,a+1),
则MK=-a2+2a+3-(a+1)
=-(a-![]() )2+
)2+![]() ,
,
根据二次函数的性质可知,当a=![]() 时,MK有最大长度
时,MK有最大长度![]() ,
,
∴S△AMB最大=S△AMK+S△BMK
=![]() MKAH+
MKAH+![]() MK(xB-xH)
MK(xB-xH)
=![]() MK(xB-xA)
MK(xB-xA)
=![]() ×
×![]() ×3
×3
=![]() ,
,
∴以MA、MB为相邻的两边作平行四边形MANB,当平行四边形MANB的面积最大时,
S最大=2S△AMB最大=2×![]() =
=![]() ,M(
,M(![]() ,
,![]() );
);
(3)存在点F,
∵y=-x2+2x+3
=-(x-1)2+4,
∴对称轴为直线x=1,
当y=0时,x1=-1,x2=3,
∴抛物线与点x轴正半轴交于点C(3,0),
如图2,分别过点B,C作直线y=![]() 的垂线,垂足为N,H,
的垂线,垂足为N,H,
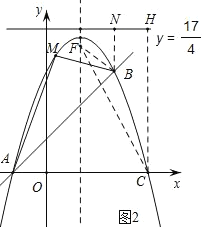
抛物线对称轴上存在点F,使抛物线C上任意一点P到点F的距离等于到直线y=![]() 的距离,设F(1,a),连接BF,CF,
的距离,设F(1,a),连接BF,CF,
则BF=BN=![]() -3=
-3=![]() ,CF=CH=
,CF=CH=![]() ,
,
由题意可列: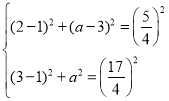 ,
,
解得,a=![]() ,
,
∴F(1,![]() ).
).


科目:初中数学 来源: 题型:
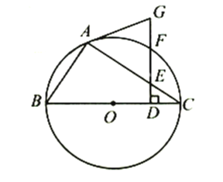
【题目】如图,![]() 为⊙
为⊙![]() 的内接三角形,
的内接三角形,![]() 为⊙
为⊙![]() 的直径,在线段
的直径,在线段![]() 上取点
上取点![]() (不与端点重合),作
(不与端点重合),作![]() ,分别交
,分别交![]() 、圆周于
、圆周于![]() 、
、![]() ,连接
,连接![]() ,已知
,已知![]() .
.
(1)求证:![]() 为⊙
为⊙![]() 的切线;
的切线;
(2)已知![]() ,填空:
,填空:
①当![]() __________
__________![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②若![]() ,当
,当![]() __________时,
__________时,![]() 为等腰直角三角形.
为等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为![]() .
.
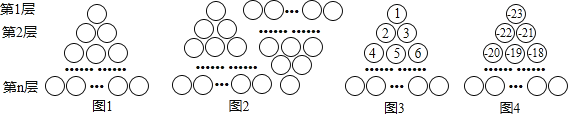
如果图中的圆圈共有13层,请问:自上往下,在每个圆圈中按图3的方式填上一串连续的正整数1,2,3,4,……,则最底层最左边这个圆圈中的数是__________;自上往下,在每个圆圈中按图4的方式填上一串连续的整数﹣23,﹣22,﹣21,﹣20,……,则所有圆圈中各数的绝对值之和为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
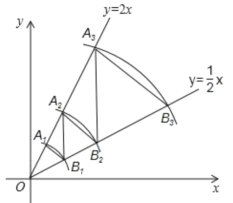
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 长为半径画弧,交直线
长为半径画弧,交直线![]() 于点
于点![]() ,过
,过![]() 点作
点作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,以
,以![]() 为圆心,以
为圆心,以![]() 长为半径画弧,交直线
长为半径画弧,交直线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 长为半径画弧,交直线
长为半径画弧,交直线![]() 于点
于点![]() ,过
,过![]() 点作
点作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 长为半径面弧,交直线
长为半径面弧,交直线![]() 于点
于点![]() ,…,按照如此规律进行下去,点
,…,按照如此规律进行下去,点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的对称轴是直线x=﹣2.抛物线与x轴的一个交点在点(﹣4,0)和点(﹣3,0)之间,其部分图象如图所示,下列结论中正确的个数有( )①4a﹣b=0;②c≤3a;③关于x的方程ax2+bx+c=2有两个不相等实数根;④b2+2b>4ac.
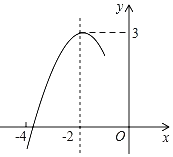
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形![]() 中,点
中,点![]() 为对角线
为对角线![]() 上一动点(点
上一动点(点![]() 与点
与点![]() 、
、![]() 不重合),连接
不重合),连接![]() ,作
,作![]() 交射线
交射线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() 、
、![]() ,作射线
,作射线![]() 交射线
交射线![]() 于点
于点![]()
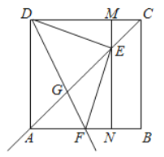
(1)求证:![]() ;
;
(2)当![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
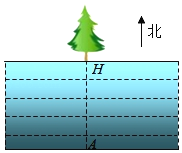
【题目】为了测量一条两岸平行的河流宽度,三个数学研究小组设计了不同的方案,他们在河南岸的点A处测得河北岸的树H恰好在A的正北方向.测量方案与数据如下表:
课题 | 测量河流宽度 | ||
测量工具 | 测量角度的仪器,皮尺等 | ||
测量小组 | 第一小组 | 第二小组 | 第三小组 |
测量方案示意图 |
|
|
|
说明 | 点B,C在点A的正东方向 | 点B,D在点A的正东方向 | 点B在点A的正东方向,点C在点A的正西方向. |
测量数据 | BC=60m, ∠ABH=70°, ∠ACH=35°. | BD=20m, ∠ABH=70°, ∠BCD=35°. | BC=101m, ∠ABH=70°, ∠ACH=35°. |
(1)哪个小组的数据无法计算出河宽?
(2)请选择其中一个方案及其数据求出河宽(精确到0.1m).(参考数据:sin70°≈0.94,sin35°≈0.57,tan70°≈2.75,tan35°≈0.70)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组建了书法、音乐、美术、舞蹈、演讲5个社团,随机调查了部分学生.被调查学生每人都参加且只参加了其中一个社团活动,并将调查结果制成了如图两幅不完整的统计图,在扇形统计图中,“音乐”所对应的扇形圆心角度数是( )度.
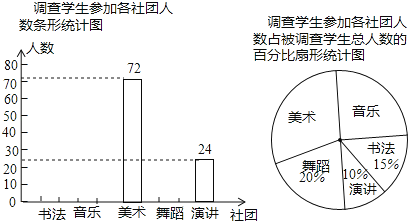
A.25%B.25C.60D.90
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com