
【题目】图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为![]() .
.
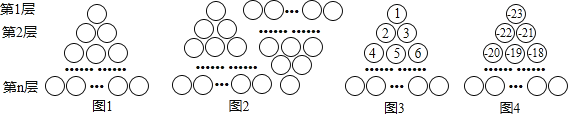
如果图中的圆圈共有13层,请问:自上往下,在每个圆圈中按图3的方式填上一串连续的正整数1,2,3,4,……,则最底层最左边这个圆圈中的数是__________;自上往下,在每个圆圈中按图4的方式填上一串连续的整数﹣23,﹣22,﹣21,﹣20,……,则所有圆圈中各数的绝对值之和为__________.
【答案】79 2554
【解析】
13层时最底层最左边这个圆圈中的数是第12层的最后一个数加1;首先计算圆圈的个数,用23+数的个数减去1就是最底层最右边圆圈内的数,再把所有数的绝对值相加即可.
解:当有13层时,图3中到第12层共有:1+2+3+…+11+12=78个圆圈,
最底层最左边这个圆圈中的数是:78+1=79;
图4中所有圆圈中共有![]() 个数,
个数,
最底层最右边圆圈内的数是﹣23+91﹣1=67;
图4中共有91个数,其中23个负数,1个0,67个正数,
所以图4中所有圆圈中各数的绝对值之和为:
|﹣23|+|﹣22|+…+|﹣1|+0+1+2+…+67
=(1+2+3+…+23)+(1+2+3+…+67)
=276+2278
=2554.
故答案为:(1)79;(2)2554.


科目:初中数学 来源: 题型:
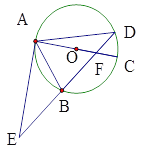
【题目】如图,已知⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB;
(1)求证:AE是⊙O的切线;
(2)已知点B是EF的中点,求证:△EAF∽△CBA
(3)已知AF=4,CF=2,在(2)的条件下,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
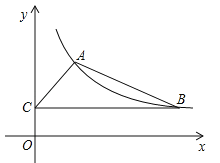
【题目】如图,某反比例函数图象的一支经过点A(2,3)和点B(点B在点A的右侧),作BC⊥y轴,垂足为点C,连结AB,AC.
(1)求该反比例函数的解析式;
(2)若△ABC的面积为6,求直线AB的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
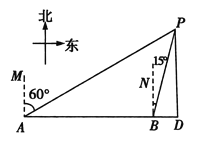
【题目】一艘轮船向正东方向航行,在A处测得灯塔P在A的北偏东60°方向,航行40海里到达B处,此时测得灯塔P在B的北偏东15°方向.
(1)求灯塔P到轮船航线的距离PD;(结果保留根号)
(2)当轮船从B处继续向东航行时,一艘快艇从灯塔P处同时前往D处,尽管快艇速度是轮船速度的2倍,但快艇还是比轮船晚15分钟到达D处,求轮船每小时航行多少海里.(结果精确到1海里,参考数据![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,对称轴为直线
,对称轴为直线![]() ,
,![]() ,下列结论:①
,下列结论:①![]() ;②9a+3b+c=0;③若点
;②9a+3b+c=0;③若点![]() ,点
,点![]() 是此函数图象上的两点,则
是此函数图象上的两点,则![]() ;④
;④![]() .其中正确的个数( )
.其中正确的个数( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A(1,0)作x轴的垂线与直线y=x相交于点B,以原点O为圆心、OA为半径的圆与y轴相交于点C、D,抛物线y=x2+px+q经过点B、C.
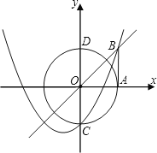
(1)求p、q的值;
(2)设抛物线的对称轴与x轴相交于点E,连接CE并延长与⊙O相交于点F,求EF的长;
(3)记⊙O与x轴负半轴的交点为G,过点D作⊙O的切线与CG的延长线相交于点H.点H是否在抛物线上?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() :
:![]() 相交于
相交于![]() 和点
和点![]() 两点.
两点.
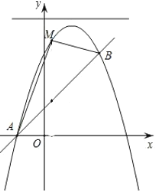
⑴求抛物线![]() 的函数表达式;
的函数表达式;
⑵若点![]() 是位于直线
是位于直线![]() 上方抛物线上的一动点,以
上方抛物线上的一动点,以![]() 为相邻两边作平行四边形
为相邻两边作平行四边形![]() ,当平行四边形
,当平行四边形![]() 的面积最大时,求此时四边形
的面积最大时,求此时四边形![]() 的面积
的面积![]() 及点
及点![]() 的坐标;
的坐标;
⑶在抛物线![]() 的对称轴上是否存在定点
的对称轴上是否存在定点![]() ,使抛物线
,使抛物线![]() 上任意一点
上任意一点![]() 到点
到点![]() 的距离等于到直线
的距离等于到直线![]() 的距离,若存在,求出定点
的距离,若存在,求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中.面积最大的三角形的斜边长是_____.
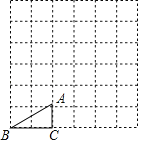
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形![]() 是矩形,点
是矩形,点![]() ,点
,点![]() ,点
,点![]() .以
.以![]() 点为中心,顺时针旋转矩形
点为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 的对应点分别为
的对应点分别为![]() ,记旋转角为
,记旋转角为![]() .
.
(1)如图①,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
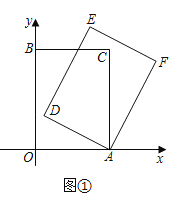
(2)如图②,当点![]() 落在
落在![]() 的延长线上时,求点
的延长线上时,求点![]() 的坐标;
的坐标;
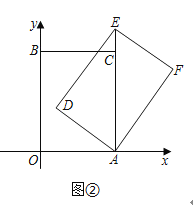
(3)当点![]() 落在线段
落在线段![]() 上时,求点
上时,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com