
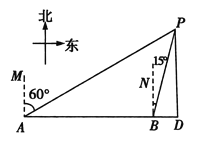
����Ŀ��һ���ִ������������У���A����õ���P��A�ı�ƫ��60��������40���ﵽ��B������ʱ��õ���P��B�ı�ƫ��15������.
(1)�����P���ִ����ߵľ���PD��(�����������)
(2)���ִ���B����������ʱ��һ�ҿ�ͧ�ӵ���P��ͬʱǰ��D�������ܿ�ͧ�ٶ����ִ��ٶȵ�2��������ͧ���DZ��ִ���15���ӵ���D�������ִ�ÿСʱ���ж��ٺ���.(�����ȷ��1����ο�����![]() ��1.7)
��1.7)
���𰸡���1������P���ִ����ߵľ���PD��(10��10![]() )�����2���ִ�ÿСʱԼ����26����.
)�����2���ִ�ÿСʱԼ����26����.
��������
��1������B��BC��AP�ڵ�C�������BC��AC�ij��ȣ�Ȼ��ȷ����CBP�Ķ������̶���ֱ��������PAD�п��������PD��
��2�����ִ�ÿСʱ����x�����Rt��ADP�����AD���̶���ʾ��BD���г����̿ɽ��x��ֵ��
�⣺(1)����B��BC��AP�ڵ�C.
��Rt��ABC����ACB=90������BAC=30����
��BC=![]() AB=20���AC=AB��cos30��=20
AB=20���AC=AB��cos30��=20![]() ����.
����.
�ߡ�PBD=90����15��=75������ABC=90����30��=60����
���CBP=180����75����60��=45����
��PC=BC=20���
��AP=PC��AC=(20��20![]() )����.
)����.
��PD��AD����PAD=30����
��PD=![]() AP=(10��10
AP=(10��10![]() )����.
)����.
��ˣ�����P���ִ����ߵľ���PD��(10��10![]() )����.
)����.
(2)���ִ�ÿСʱ����x���
��Rt��ADP��AD=AP��cos30��=![]() �� (20��20
�� (20��20![]() )=(30��10
)=(30��10![]() )(����)��
)(����)��
��BD=AD��AB=30��10![]() ��40=(10
��40=(10![]() ��10)(����)��
��10)(����)��
�����⣬��![]() ��
��![]() =
=![]() ��
��
���x=60��20![]() ��
��
������x=60��20![]() ��ԭ���̵Ľ⣬
��ԭ���̵Ľ⣬
��x=60��20![]() ��26.
��26.
��ˣ��ִ�ÿСʱԼ����26����.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BC�ǡ�O�����ߣ�D���е㣮����BO���ӳ�������O�ڵ�E��A����A��AC��BC������ΪC����BD��8��BE��4����AC��_____��
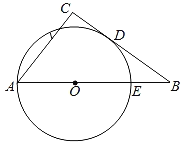
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2020�괺����ѧ��,ijУ�ƶ��ˡ��¹ڷ�����������ڼ�Ͳ淶���������涨��������Ͳ͡�ʳ���������Ͳ͡���������ȾͲʹ�ʩ��Ϊ�˽�ѧ���Թ淶����֪�̶ȣ�УС����������鲿��ͬѧ�������ݵ���������������������������ͳ��ͼ����

���������ͼ��������������⣺
��1����α������ͬѧ����______�ˣ�![]() ______��
______��![]() ______��
______��
��2��������ͳ��ͼ��B��������Բ�ĽǶ�����
��3��ѧУ��ί�����̴����ԡ���̫�˽⡱��������֪�顱��ͬѧ������ѧϰ��ѵ��������У2400��ѧ����Ԥ���ж�����Ҫ������ѧϰ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У�����ABCO�ı�OA��x���ϣ���OC��y���ϣ���B������Ϊ��1��3�����������ضԽ���AC���ۣ�B������D���λ�ã���AD��y���ڵ�E����ô��D������Ϊ��������
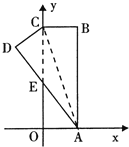
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��O�İ뾶��4����A,B,C�ڡ�O�ϣ����ı���OABCΪ���Σ���ͼ����Ӱ�������Ϊ�� ��
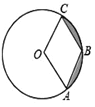
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����Rt��ABC�У���B��90����AC��60cm����A��60������D�ӵ�C������CA������4cm/s���ٶ����A�����˶���ͬʱ��E�ӵ�A������AB������2cm/s���ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����ts��0��t��15��������D��DF��BC�ڵ�F������DE��EF�����ı���AEFDΪ���Σ���t��ֵΪ�� ��
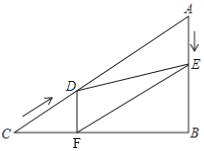
A.20B.15C.10D.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1�������ɸ�СԲȦ�ѳɵ�һ������ȱ������ε�ͼ����������һ����һ��ԲȦ�����¸��������һ���һ��ԲȦ��һ������n�㣮��ͼ1���ú���ԭͼ1ƴ��ͼ2����״���������ǿ������ͼ1������ԲȦ�ĸ���Ϊ![]() ��
��
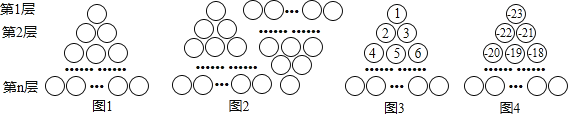
���ͼ�е�ԲȦ����13�㣬���ʣ��������£���ÿ��ԲȦ�а�ͼ3�ķ�ʽ����һ��������������1��2��3��4������������ײ���������ԲȦ�е�����__________���������£���ÿ��ԲȦ�а�ͼ4�ķ�ʽ����һ��������������23����22����21����20��������������ԲȦ�и����ľ���ֵ֮��Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y��ax2+bx+c�ĶԳ�����ֱ��x����2����������x���һ�������ڵ㣨��4��0���͵㣨��3��0��֮�䣬�䲿��ͼ����ͼ��ʾ�����н�������ȷ�ĸ����У���������4a��b��0����c��3a���۹���x�ķ���ax2+bx+c��2�����������ʵ��������b2+2b��4ac��
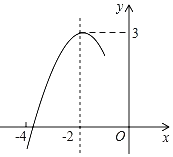
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
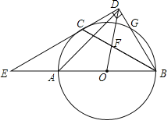
����Ŀ����ͼ��ABΪ��O��ֱ����C��G�ǡ�O�����㣬�һ�AC����CG������C��ֱ��CD��BG�ڵ�D����BA���ӳ����ڵ�E������BC����OD�ڵ�F��
��1����֤��CD�ǡ�O�����ߣ�
��2����![]() ����AD�ij���
����AD�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com