
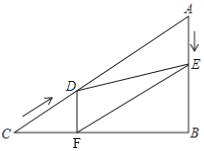
【题目】如图所示,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D,E运动的时间是ts(0<t≤15),过点D作DF⊥BC于点F,连接DE,EF,若四边形AEFD为菱形,则t的值为( )
A.20B.15C.10D.5
科目:初中数学 来源: 题型:
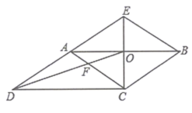
【题目】如图,CE是平行四边形ABCD的边AB的垂直平分线,垂足为点![]() ,CE与DA的延长线交于点E,连接AC,BE,DO,DO与AC交于点F,则下列结论:①四边形ACBE是菱形;②
,CE与DA的延长线交于点E,连接AC,BE,DO,DO与AC交于点F,则下列结论:①四边形ACBE是菱形;②![]() ;③
;③![]() ;④S四边形AFOE:
;④S四边形AFOE:![]() ,其中正确的结论有( )
,其中正确的结论有( )
A.①②③B.①②④C.①②D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
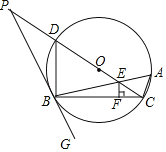
【题目】如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD.
(1)求证:PG与⊙O相切;
(2)若![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,若⊙O的半径为8,PD=OD,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
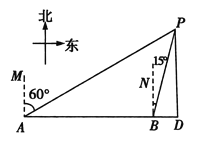
【题目】一艘轮船向正东方向航行,在A处测得灯塔P在A的北偏东60°方向,航行40海里到达B处,此时测得灯塔P在B的北偏东15°方向.
(1)求灯塔P到轮船航线的距离PD;(结果保留根号)
(2)当轮船从B处继续向东航行时,一艘快艇从灯塔P处同时前往D处,尽管快艇速度是轮船速度的2倍,但快艇还是比轮船晚15分钟到达D处,求轮船每小时航行多少海里.(结果精确到1海里,参考数据![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
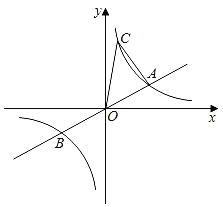
【题目】如图,已知直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0)交于A、B两点,A点的横坐标为3,则下列结论:①k=6;②A点与B点关于原点O中心对称;③关于x的不等式
(k>0)交于A、B两点,A点的横坐标为3,则下列结论:①k=6;②A点与B点关于原点O中心对称;③关于x的不等式![]() <0的解集为x<﹣3或0<x<3;④若双曲线y=
<0的解集为x<﹣3或0<x<3;④若双曲线y=![]() (k>0)上有一点C的纵坐标为6,则△AOC的面积为8,其中正确结论的个数( )
(k>0)上有一点C的纵坐标为6,则△AOC的面积为8,其中正确结论的个数( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A(1,0)作x轴的垂线与直线y=x相交于点B,以原点O为圆心、OA为半径的圆与y轴相交于点C、D,抛物线y=x2+px+q经过点B、C.
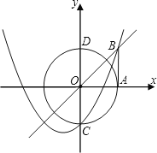
(1)求p、q的值;
(2)设抛物线的对称轴与x轴相交于点E,连接CE并延长与⊙O相交于点F,求EF的长;
(3)记⊙O与x轴负半轴的交点为G,过点D作⊙O的切线与CG的延长线相交于点H.点H是否在抛物线上?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
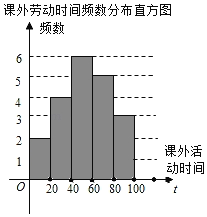
【题目】遵义市各校都在深入开展劳动教育,某校为了解七年级学生一学期参加课外劳动时间(单位:h)的情况,从该校七年级随机抽查了部分学生进行问卷调查,并将调查结果绘制成如下不完整的频数分布表和频数分布直方图.
课外劳动时间频数分布表
劳动时间分组 | 频数 | 频率 |
0≤t<20 | 2 | 0.1 |
20≤t<40 | 4 | m |
40≤t<60 | 6 | 0.3 |
60≤t<80 | a | 0.25 |
80≤t<100 | 3 | 0.15 |
解答下列问题:
(1)频数分布表中a= ,m= ;将频数分布直方图补充完整;
(2)若七年级共有学生400人,试估计该校七年级学生一学期课外劳动时间不少于60h的人数;
(3)已知课外劳动时间在60h≤t<80h的男生人数为2人,其余为女生,现从该组中任选2人代表学校参加“全市中学生劳动体验”演讲比赛,请用树状图或列表法求所选学生为1男1女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com