
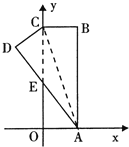
【题目】如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E。那么点D的坐标为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】
如图,过D作DF⊥AF于F,根据折叠可以证明△CDE≌△AOE,然后利用全等三角形的性质得到OE=DE,OA=CD=1,设OE=x,那么CE=3-x,DE=x,利用勾股定理即可求出OE的长度,而利用已知条件可以证明△AEO∽△ADF,而AD=AB=3,接着利用相似三角形的性质即可求出DF、AF的长度,也就求出了D的坐标.
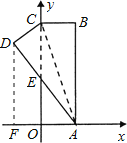
解:如图,过D作DF⊥AF于F,
∵点B的坐标为(1,3),
∴AO=1,AB=3,
根据折叠可知:CD=OA,
而∠ADC=∠AOE=90°,∠DEC=∠AEO,
∴△CDE≌△AOE,
∴OE=DE,OA=CD=1,
设OE=x,那么CE=3-x,DE=x,
∴在Rt△DCE中,CE2=DE2+CD2,
∴(3-x)2=x2+12,
∴x=![]() ,
,
又DF⊥AF,
∴DF∥EO,
∴△AEO∽△ADF,
而AD=AB=3,
∴AE=CE=3-![]() =
=![]() ,
,
∴![]() ,
,
即![]() ,
,
∴DF=![]() ,AF=
,AF=![]() ,
,
∴OF=![]() -1=
-1=![]() ,
,
∴D的坐标为(-![]() ,
, ![]() ).
).
故选A.
【地哪家】
本题主要考查了图形的折叠问题,也考查了坐标与图形的性质,解题的关键是把握折叠的隐含条件,利用隐含条件得到全等三角形和相似三角形,然后利用它们的性质即可解决问题.


科目:初中数学 来源: 题型:
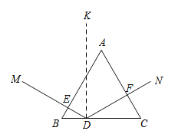
【题目】如图所示,边长为2的等边△ABC是三棱镜的一个横截面.一束光线ME沿着与AB边垂直的方向射入到BC边上的点D处(点D与B,C不重合),反射光线沿DF的方向射出去,DK与BC垂直,且入射光线和反射光线使∠MDK=∠FDK.设BE的长为x,△DFC的面积为y,则下列图象中能大致表示y与x的函数关系的是( )
A. B.
B.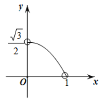 C.
C.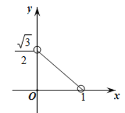 D.
D.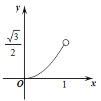
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别是
分别是![]() 的中点,连接
的中点,连接![]() .
.
(1)探索发现:
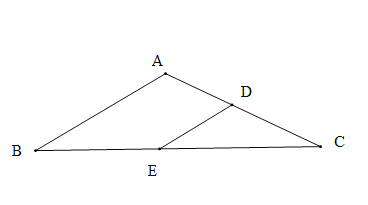
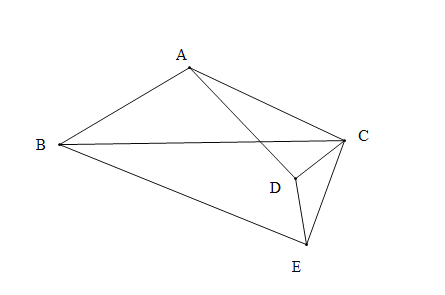
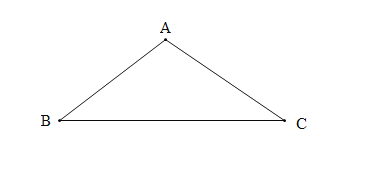
图1中,![]() 的值为_____________;
的值为_____________;![]() 的值为_________.
的值为_________.
(2)拓展探究
若将![]() 绕点
绕点![]() 逆时针方向旋转一周,在旋转过程中
逆时针方向旋转一周,在旋转过程中![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
当![]() 旋转至
旋转至![]() 三点在同一直线时,直接写出线段
三点在同一直线时,直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CE是平行四边形ABCD的边AB的垂直平分线,垂足为点![]() ,CE与DA的延长线交于点E,连接AC,BE,DO,DO与AC交于点F,则下列结论:①四边形ACBE是菱形;②
,CE与DA的延长线交于点E,连接AC,BE,DO,DO与AC交于点F,则下列结论:①四边形ACBE是菱形;②![]() ;③
;③![]() ;④S四边形AFOE:
;④S四边形AFOE:![]() ,其中正确的结论有( )
,其中正确的结论有( )
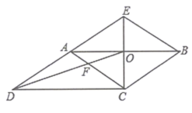
A.①②③B.①②④C.①②D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
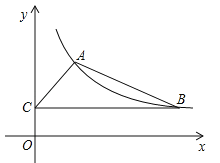
【题目】如图,某反比例函数图象的一支经过点A(2,3)和点B(点B在点A的右侧),作BC⊥y轴,垂足为点C,连结AB,AC.
(1)求该反比例函数的解析式;
(2)若△ABC的面积为6,求直线AB的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
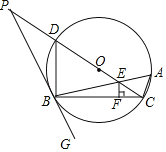
【题目】如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD.
(1)求证:PG与⊙O相切;
(2)若![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,若⊙O的半径为8,PD=OD,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
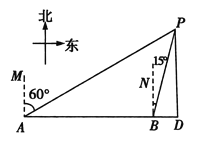
【题目】一艘轮船向正东方向航行,在A处测得灯塔P在A的北偏东60°方向,航行40海里到达B处,此时测得灯塔P在B的北偏东15°方向.
(1)求灯塔P到轮船航线的距离PD;(结果保留根号)
(2)当轮船从B处继续向东航行时,一艘快艇从灯塔P处同时前往D处,尽管快艇速度是轮船速度的2倍,但快艇还是比轮船晚15分钟到达D处,求轮船每小时航行多少海里.(结果精确到1海里,参考数据![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A(1,0)作x轴的垂线与直线y=x相交于点B,以原点O为圆心、OA为半径的圆与y轴相交于点C、D,抛物线y=x2+px+q经过点B、C.
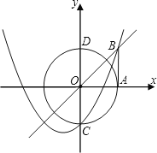
(1)求p、q的值;
(2)设抛物线的对称轴与x轴相交于点E,连接CE并延长与⊙O相交于点F,求EF的长;
(3)记⊙O与x轴负半轴的交点为G,过点D作⊙O的切线与CG的延长线相交于点H.点H是否在抛物线上?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在九年级“线上教学”结束后,为了解学生的视力情况,抽查了部分学生进行视力检测.根据检测结果,制成下面不完整的统计图表.
被抽样的学生视力情况频数表
组别 | 视力段 | 频数 |
A | 5.1≤x≤5.3 | 25 |
B | 4.8≤x≤5.0 | 115 |
C | 4.4≤x≤4.7 | m |
D | 4.0≤x≤4.3 | 52 |
(1)求组别C的频数m的值.
(2)求组别A的圆心角度数.
(3)如果视力值4.8及以上属于“视力良好”,请估计该市25000名九年级学生达到“视力良好”的人数.根据上述图表信息,你对视力保护有什么建议?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com