
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别是
分别是![]() 的中点,连接
的中点,连接![]() .
.
(1)探索发现:
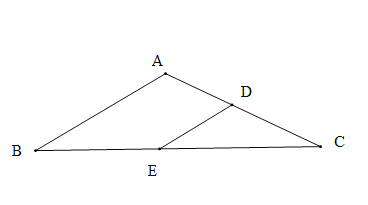
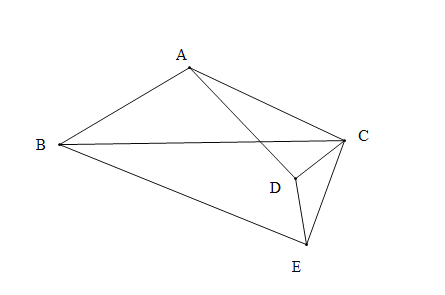
图1中,![]() 的值为_____________;
的值为_____________;![]() 的值为_________.
的值为_________.
(2)拓展探究
若将![]() 绕点
绕点![]() 逆时针方向旋转一周,在旋转过程中
逆时针方向旋转一周,在旋转过程中![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
当![]() 旋转至
旋转至![]() 三点在同一直线时,直接写出线段
三点在同一直线时,直接写出线段![]() 的长.
的长.
【答案】(1)![]() ;
;![]() (2)见解析 (3)
(2)见解析 (3)![]() 或
或![]()
【解析】
(1)先判断出∠AEB=90°,再判断出∠B=30°,进而的粗AE,再用勾股定理求出BE,即可得出结论;
(2)先判断出,进而得出△ACD∽△BCE,即可得出结论;
(3)分点D在线段AE上和AE的延长线上,利用含30度角的直角三角形的性质和勾股定理,最后用线段的和差求出AD,即可得出结论.
解:
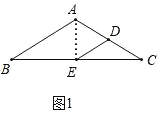
解: (1)如图1,连接AE,
∵AB=AC=2,点E分别是BC的中点,
∴AE⊥ BC,
∴∠AEC=90° ,
∵AB=AC=2,∠BAC=120° ,
∴∠B=∠C=30°,
在Rt△ABE中,AE=![]() AB=1,根据勾股定理得,BE
AB=1,根据勾股定理得,BE![]()
∵点E是BC的中点,
∴BC=2BE![]()
∴![]()
∵点D是AC的中点,
∴AD=CD=![]() AC=1,
AC=1,
∴![]()
故答案为:![]() ,
,![]() ;
;
(2)无变化,理由:
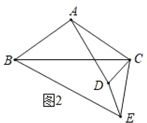
由(1)知,CD=1,![]() ,
,
∴![]() ,
,![]()
∴![]() ,
,
由(1)知,∠ACB=∠DCE=30°,
∴∠ACD=∠BCE,
∴△ACD∽△BCE,
∴![]() ,
,
(3)线段BE的长为![]() 或
或![]() ,理由如下:
,理由如下:
当点D在线段AE上时,
如图2,过点C作CF⊥AE于F,∠CDF=180°﹣∠CDE=60°,
∴∠DCF=30°,
∴![]() ,
,
∴![]() ,
,
在Rt△AFC中,AC=2,根据勾股定理得,![]() ,
,
∴AD=AF+DF=![]() ,
,
由(2)知,![]() ,
,
∴![]()
当点D在线段AE的延长线上时,
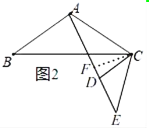
如图3,过点C作CG⊥AD交AD的延长线于G,
∵∠CDG=60°,
∴∠DCG=30°,
∴![]() ,
,
∴![]() ,
,
在Rt△ACG中,根据勾股定理得,![]() ,
,
∴![]() ,
,
由(2)知,![]() ,
,
∴![]()
即:线段BE的长为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (
(![]() 是常数,
是常数,![]() )与
)与![]() 轴交于
轴交于![]() 两点,顶点
两点,顶点![]() 给出下列结论:①
给出下列结论:①![]() ;②若
;②若![]() 在抛物线上,则
在抛物线上,则![]() ;③关于
;③关于![]() 的方程
的方程![]() 有实数解,则
有实数解,则![]() ;④当
;④当![]() 时,
时,![]() 为等腰直角三角形,其中正确的结论是( )
为等腰直角三角形,其中正确的结论是( )
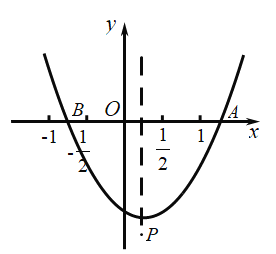
A.①②B.①③C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年1月新冠肺炎大面积爆发,大批的医护人员积极前赴武汉支援一线救治,但是大批的医用物资仍旧极度短缺,我市某中学九年级一班全体同学参加了“加油武汉,加油中国”捐款活动,该班同学捐款情况的部分统计图如图所示:
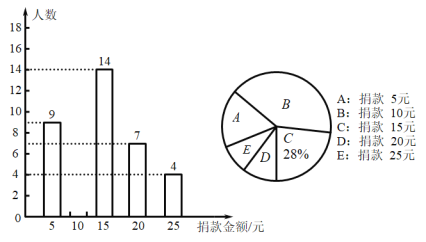
(1)求该班的总人数,将条形图补充完整.
(2)求出捐款金额的平均数、众数、中位数;
(3)若想在捐款金额为25元的四名同学![]() 、
、![]() 、
、![]() 、
、![]() 中选取2位同学负责把钱交到红十字会,请用列表法或画树形图的方法求出恰好选中
中选取2位同学负责把钱交到红十字会,请用列表法或画树形图的方法求出恰好选中![]() 、
、![]() 两名同学的概率是多少?
两名同学的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
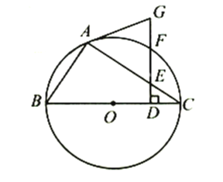
【题目】如图,![]() 为⊙
为⊙![]() 的内接三角形,
的内接三角形,![]() 为⊙
为⊙![]() 的直径,在线段
的直径,在线段![]() 上取点
上取点![]() (不与端点重合),作
(不与端点重合),作![]() ,分别交
,分别交![]() 、圆周于
、圆周于![]() 、
、![]() ,连接
,连接![]() ,已知
,已知![]() .
.
(1)求证:![]() 为⊙
为⊙![]() 的切线;
的切线;
(2)已知![]() ,填空:
,填空:
①当![]() __________
__________![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②若![]() ,当
,当![]() __________时,
__________时,![]() 为等腰直角三角形.
为等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
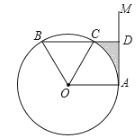
【题目】如图,点![]() 是直线
是直线![]() 与
与![]() 的交点,点
的交点,点![]() 在
在![]() 上,
上,![]() ,垂足为
,垂足为![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 平分
平分![]() ,
,![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() 的半径为4,求图中阴影部分的面积.(结果保留
的半径为4,求图中阴影部分的面积.(结果保留![]() 和根号).
和根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年春季开学后,某校制定了《新冠肺炎疫情防控期间就餐规范》,条例规定:不对面就餐、食而不语、错峰就餐、鼓励打包等就餐措施.为了解学生对规范的认知程度,校园小记者随机调查部分同学,并根据调查结果绘制了如下两幅不完整的统计图表:

请根据以上图表,解答下列问题:
(1)这次被调查的同学共有______人,![]() ______,
______,![]() ______;
______;
(2)求扇形统计图中B部分所对圆心角度数;
(3)学校团委及政教处准备对“不太了解”及“毫不知情”的同学进行再学习培训,请问我校2400名学生中预计有多少人要接受再学习?
查看答案和解析>>
科目:初中数学 来源: 题型:
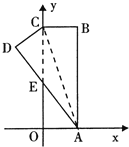
【题目】如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E。那么点D的坐标为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
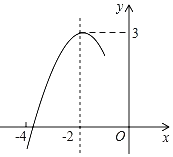
【题目】抛物线y=ax2+bx+c的对称轴是直线x=﹣2.抛物线与x轴的一个交点在点(﹣4,0)和点(﹣3,0)之间,其部分图象如图所示,下列结论中正确的个数有( )①4a﹣b=0;②c≤3a;③关于x的方程ax2+bx+c=2有两个不相等实数根;④b2+2b>4ac.
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com