
【题目】2020年1月新冠肺炎大面积爆发,大批的医护人员积极前赴武汉支援一线救治,但是大批的医用物资仍旧极度短缺,我市某中学九年级一班全体同学参加了“加油武汉,加油中国”捐款活动,该班同学捐款情况的部分统计图如图所示:
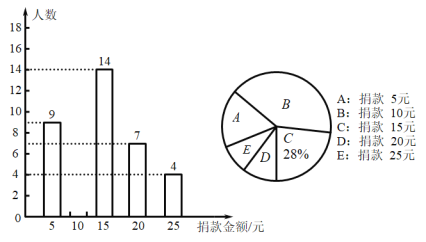
(1)求该班的总人数,将条形图补充完整.
(2)求出捐款金额的平均数、众数、中位数;
(3)若想在捐款金额为25元的四名同学![]() 、
、![]() 、
、![]() 、
、![]() 中选取2位同学负责把钱交到红十字会,请用列表法或画树形图的方法求出恰好选中
中选取2位同学负责把钱交到红十字会,请用列表法或画树形图的方法求出恰好选中![]() 、
、![]() 两名同学的概率是多少?
两名同学的概率是多少?
【答案】(1)50人,补全图形见解析;(2)平均数为13.1元,众数为10元,中位数为12.5元;(3)![]() .
.
【解析】
(1)由捐款15元的人数除以占的百分比,即可确定出该班的总人数;用总人数减去捐款为5元、15元、20元、25元的人数,即可求出捐款为10元的人数,补全条形图.
(2)平均数为捐款总数除以总人数;由条形图可知,捐款10元的人数最多,即得众数;将50名同学的捐款数从小到大排列,第25、26位同学的捐款平均数为中位数;
(3)用列表法展示所有12种等可能的结果数,再找出选中A、B两名同学的结果数,根据概率公式求解.
解:(l)该班的总人数为![]() (人),
(人),
捐款10元的人数:![]() .
.
图形补充如下图所示:
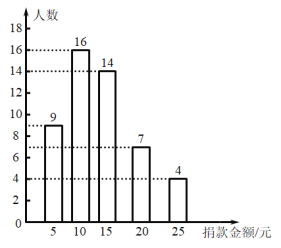
(2)平均数为:![]()
![]() (元),
(元),
众数是10元,中位数为:![]() 元
元
∴该班捐款平均数为13.1元,众数为10元,中位数为12.5元.
(3)
第一次 第二次 |
|
|
|
|
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
|
所有的等可能结果共12种,事件恰好选中![]() 、
、![]() 两位同学包含两种等可能结果.
两位同学包含两种等可能结果.
∴![]()
答:恰好选中![]() 、
、![]() 两位同学的概率为
两位同学的概率为![]() .
.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.
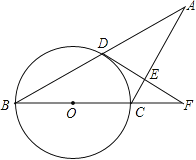
(1)求证:AD=BD;
(2)求证:DF是⊙O的切线
(3)若⊙O直径为18,![]() ,求DE的长
,求DE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,边长为2的等边△ABC是三棱镜的一个横截面.一束光线ME沿着与AB边垂直的方向射入到BC边上的点D处(点D与B,C不重合),反射光线沿DF的方向射出去,DK与BC垂直,且入射光线和反射光线使∠MDK=∠FDK.设BE的长为x,△DFC的面积为y,则下列图象中能大致表示y与x的函数关系的是( )
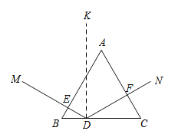
A. B.
B.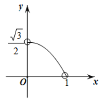 C.
C.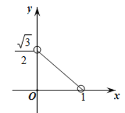 D.
D.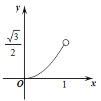
查看答案和解析>>
科目:初中数学 来源: 题型:
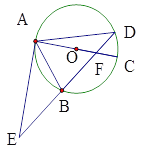
【题目】如图,已知⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB;
(1)求证:AE是⊙O的切线;
(2)已知点B是EF的中点,求证:△EAF∽△CBA
(3)已知AF=4,CF=2,在(2)的条件下,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=6,BC=4,AD是BC边上的高,AM是△ABC外角∠CAE的平分线.以点D为圆心,适当长为半径画弧,交DA于点G,交DC于点H.再分别以点G、H为圆心,大于![]() GH的长为半径画弧,两弧在∠ADC内部交于点Q,连接DQ并延长与AM交于点F,则DF的长度为( ).
GH的长为半径画弧,两弧在∠ADC内部交于点Q,连接DQ并延长与AM交于点F,则DF的长度为( ).
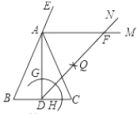
A.6B.![]() C.
C.![]() D.8
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别是
分别是![]() 的中点,连接
的中点,连接![]() .
.
(1)探索发现:
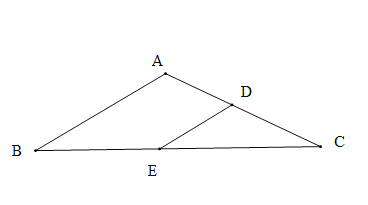
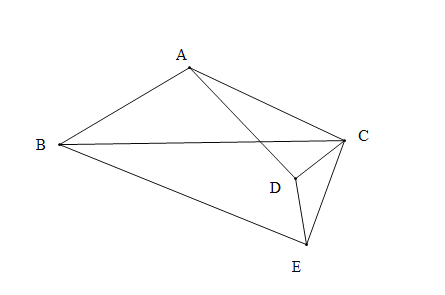
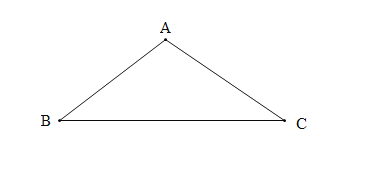
图1中,![]() 的值为_____________;
的值为_____________;![]() 的值为_________.
的值为_________.
(2)拓展探究
若将![]() 绕点
绕点![]() 逆时针方向旋转一周,在旋转过程中
逆时针方向旋转一周,在旋转过程中![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
当![]() 旋转至
旋转至![]() 三点在同一直线时,直接写出线段
三点在同一直线时,直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CE是平行四边形ABCD的边AB的垂直平分线,垂足为点![]() ,CE与DA的延长线交于点E,连接AC,BE,DO,DO与AC交于点F,则下列结论:①四边形ACBE是菱形;②
,CE与DA的延长线交于点E,连接AC,BE,DO,DO与AC交于点F,则下列结论:①四边形ACBE是菱形;②![]() ;③
;③![]() ;④S四边形AFOE:
;④S四边形AFOE:![]() ,其中正确的结论有( )
,其中正确的结论有( )
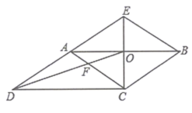
A.①②③B.①②④C.①②D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A(1,0)作x轴的垂线与直线y=x相交于点B,以原点O为圆心、OA为半径的圆与y轴相交于点C、D,抛物线y=x2+px+q经过点B、C.
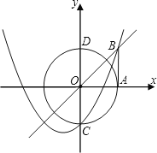
(1)求p、q的值;
(2)设抛物线的对称轴与x轴相交于点E,连接CE并延长与⊙O相交于点F,求EF的长;
(3)记⊙O与x轴负半轴的交点为G,过点D作⊙O的切线与CG的延长线相交于点H.点H是否在抛物线上?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com