
【题目】如图,抛物线![]() (
(![]() 是常数,
是常数,![]() )与
)与![]() 轴交于
轴交于![]() 两点,顶点
两点,顶点![]() 给出下列结论:①
给出下列结论:①![]() ;②若
;②若![]() 在抛物线上,则
在抛物线上,则![]() ;③关于
;③关于![]() 的方程
的方程![]() 有实数解,则
有实数解,则![]() ;④当
;④当![]() 时,
时,![]() 为等腰直角三角形,其中正确的结论是( )
为等腰直角三角形,其中正确的结论是( )
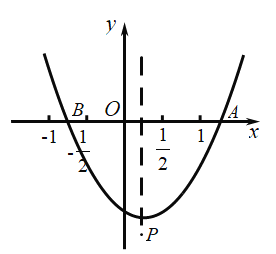
A.①②B.①③C.②③D.②④
【答案】D
【解析】
利用二次函数的图象及性质一一判断即可.
解:∵-![]() <
<![]() ,a>0,
,a>0,
∴a>-b,
∴2a=a+a>a-b
∵x=-1时,y>0,
∴a-b+c>0,
∴2a+c>a-b+c>0,故①错误;
若![]() ,
,![]() ,
,![]() 在抛物线上,
在抛物线上,
由图象法可知,y1>y2>y3;故②正确;
∵抛物线与直线y=t有交点时,方程ax2+bx+c=t有解,t≥n,
∴ax2+bx+c-t=0有实数解
要使得ax2+bx+k=0有实数解,则k=c-t≤c-n;故③错误;
设抛物线的对称轴交x轴于H.
∵![]() ,
,
∴b2-4ac=4,
∴x=![]() ,
,
∴|x1-x2|=![]() ,
,
∴AB=2PH,
∵BH=AH,
∴PH=BH=AH,
∴![]() 是直角三角形,
是直角三角形,
∵PA=PB,
∴![]() 是等腰直角三角形,故④正确.
是等腰直角三角形,故④正确.
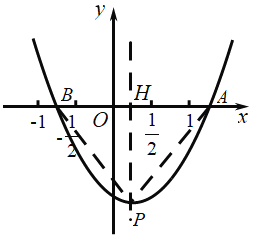
故选D.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:初中数学 来源: 题型:
【题目】每年端午节期间,小华都要自制 A、B 两种类型的粽子在线上线下进行销售,今年他经过市场调查发现,若制作 3 个 A 型粽子 2 个 B 型粽子需成本 11 元,若制作 2 个 A 型粽子 3 个B 型粽子需成本 11.5 元.
(1)求今年制作 A、B 两种类型的粽子每个的成本分别是多少元?
(2)由于今年的疫情,小华预计网上销售会大增,所以决定制作 A 型粽子 2000 个,B 型粽子 1000 个,并且统一售价每个 4 元,销售一段时间后,随着端午节的临近,小华把剩余的粽子打 8 折全部通过线上线下两种方式售出,在制作和销售过程中还产生了除成本以外其它费用合计 700 元,小华在这次买卖中赚到至少 4000 元,则打折销售的粽子最多是多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
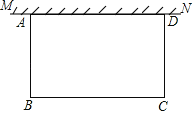
【题目】如图,在足够大的空地上有一段长为a(a≥50)米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.
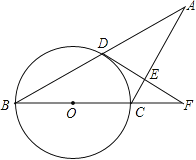
(1)求证:AD=BD;
(2)求证:DF是⊙O的切线
(3)若⊙O直径为18,![]() ,求DE的长
,求DE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A、B在直线MN上(A在B的左侧),点P是直线MN上方一点.若∠PAN=x°,∠PBN=y°,记< x,y >为P的双角坐标.例如,若△PAB是等边三角形,则点P的双角坐标为< 60,120 >.
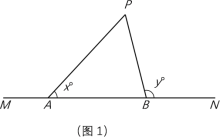

(1)如图2,若AB=22 cm,P<26.6,58>,求△PAB的面积;
(参考数据:tan26.6°≈0.50,tan58°≈1.60.)
(2)在图3中用直尺和圆规作出点P < x,y >,其中y=2x且y=x+30.(保留作图痕迹)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:
我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.
求证:BD是四边形ABCD的“相似对角线”;
(3)如图3,已知FH是四边形EFCH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为2![]() ,求FH的长.
,求FH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
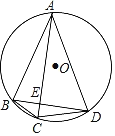
【题目】如图,四边形ABCD内接于⊙O,AC⊥BD于E.
(1)用尺规作图作DF⊥AB于F,交AC于G,并标出F、G(保留作图痕迹,不写作法);
(2)在(1)中,若∠BAD=45°,求证:EG=EC.
查看答案和解析>>
科目:初中数学 来源: 题型:
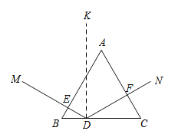
【题目】如图所示,边长为2的等边△ABC是三棱镜的一个横截面.一束光线ME沿着与AB边垂直的方向射入到BC边上的点D处(点D与B,C不重合),反射光线沿DF的方向射出去,DK与BC垂直,且入射光线和反射光线使∠MDK=∠FDK.设BE的长为x,△DFC的面积为y,则下列图象中能大致表示y与x的函数关系的是( )
A. B.
B.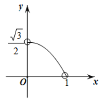 C.
C.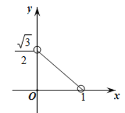 D.
D.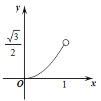
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别是
分别是![]() 的中点,连接
的中点,连接![]() .
.
(1)探索发现:
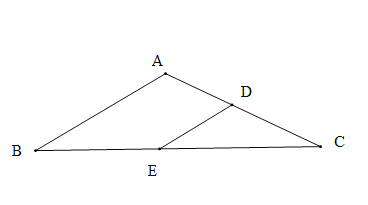
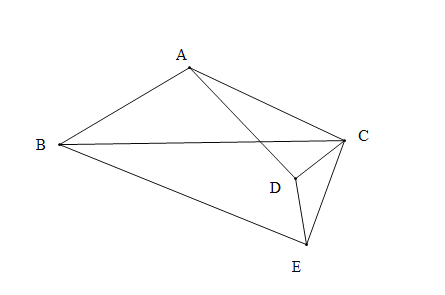
图1中,![]() 的值为_____________;
的值为_____________;![]() 的值为_________.
的值为_________.
(2)拓展探究
若将![]() 绕点
绕点![]() 逆时针方向旋转一周,在旋转过程中
逆时针方向旋转一周,在旋转过程中![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
当![]() 旋转至
旋转至![]() 三点在同一直线时,直接写出线段
三点在同一直线时,直接写出线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com