
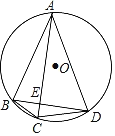
【题目】如图,四边形ABCD内接于⊙O,AC⊥BD于E.
(1)用尺规作图作DF⊥AB于F,交AC于G,并标出F、G(保留作图痕迹,不写作法);
(2)在(1)中,若∠BAD=45°,求证:EG=EC.
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,已知∠ACB=90°,AC=BC=4,若点E在△ABC内部运动,且满足AE2=BE2+2CE2,则点E的运动路径长是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家经营打印耗材的门店经销各种打印耗材,其中某一品牌硒鼓的进价为![]() 元/个,售价为
元/个,售价为![]() 元/个(
元/个(![]() ).下面是门店在销售一段时间后销售情况的反馈:
).下面是门店在销售一段时间后销售情况的反馈:
①若每个硒鼓按定价30元的8折出售,可获![]() 的利润;
的利润;
②如果硒鼓按30元/个的价格出售,每月可售出500个,在此基础上,售价每增加5元,月销售量就减少50个.
(1)求![]() 的值,并写出该品牌硒鼓每月的销售量
的值,并写出该品牌硒鼓每月的销售量![]() (个)与售价
(个)与售价![]() (元/个)之间的函数关系式,并注明自变量
(元/个)之间的函数关系式,并注明自变量![]() 的取值范围;
的取值范围;
(2)求该耗材店销售这种硒鼓每月获得的利润![]() (元)与售价
(元)与售价![]() (元/个)之间的函数关系式,并求每月获得的最大利润;
(元/个)之间的函数关系式,并求每月获得的最大利润;
(3)在新冠肺炎流行期间,这种硒鼓的进价降低为![]() 元/个,售价为
元/个,售价为![]() 元/个(
元/个(![]() ).耗材店在2月份仍然按照销售量与售价关系不变的方式销售,并决定将当月销售这种硒鼓获得的利润全部捐赠给火神山医院,支援武汉抗击新冠肺炎.若要使这个月销售这种硒鼓获得的利润
).耗材店在2月份仍然按照销售量与售价关系不变的方式销售,并决定将当月销售这种硒鼓获得的利润全部捐赠给火神山医院,支援武汉抗击新冠肺炎.若要使这个月销售这种硒鼓获得的利润![]() (元)随售价
(元)随售价![]() (元/个)的增大而增大,请直接写出
(元/个)的增大而增大,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (
(![]() 是常数,
是常数,![]() )与
)与![]() 轴交于
轴交于![]() 两点,顶点
两点,顶点![]() 给出下列结论:①
给出下列结论:①![]() ;②若
;②若![]() 在抛物线上,则
在抛物线上,则![]() ;③关于
;③关于![]() 的方程
的方程![]() 有实数解,则
有实数解,则![]() ;④当
;④当![]() 时,
时,![]() 为等腰直角三角形,其中正确的结论是( )
为等腰直角三角形,其中正确的结论是( )
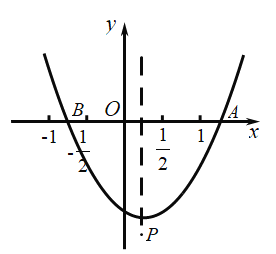
A.①②B.①③C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1.
(1)求抛物线L的解析式;
(2)将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围;
(3)设点P是抛物线L上任一点,点Q在直线l:x=﹣3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y=![]() (x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )

A. 6![]() B. 10 C. 2
B. 10 C. 2![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2008年5月1日,目前世界上最长的跨海大桥——杭州湾跨海大桥通车了.通车后,苏南A地到宁波港的路程比原来缩短了120千米.已知运输车速度不变时,行驶时间将从原来的3时20分缩短到2时.
(1)求跨海大桥到宁波港的路程.
(2)若货物运输费用=A地经杭州湾包括运输成本和时间成本,已知某车货物从A地到宁波港的运输成本是每千米1.8元,时间成本是每时28元,那么该车货物从A地经杭州湾跨海大桥到宁波港的运输费用是多少元?
(3)A地准备开辟宁波方向的外运路线,即货物从A地经杭州湾跨海大桥到宁波港,再从宁波港运到B地.若有一批货物(不超过10车)从A地按外运路线运到B地的运费需8320元,其中从A地经杭州湾跨海大桥到宁波港的每车运输费用与(2)中相同,从宁波港到B地的海上运费对一批不超过10车的货物计费方式是:一车800元,当货物每增加1车时,每车的海上运费就减少20元,问这批货物有几车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年春季开学后,某校制定了《新冠肺炎疫情防控期间就餐规范》,条例规定:不对面就餐、食而不语、错峰就餐、鼓励打包等就餐措施.为了解学生对规范的认知程度,校园小记者随机调查部分同学,并根据调查结果绘制了如下两幅不完整的统计图表:

请根据以上图表,解答下列问题:
(1)这次被调查的同学共有______人,![]() ______,
______,![]() ______;
______;
(2)求扇形统计图中B部分所对圆心角度数;
(3)学校团委及政教处准备对“不太了解”及“毫不知情”的同学进行再学习培训,请问我校2400名学生中预计有多少人要接受再学习?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com