
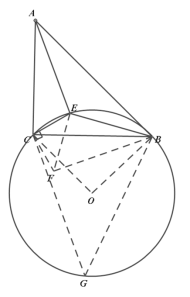
【题目】在Rt△ABC中,已知∠ACB=90°,AC=BC=4,若点E在△ABC内部运动,且满足AE2=BE2+2CE2,则点E的运动路径长是__________.
【答案】![]()
【解析】
过C作CF⊥CE且CE=CF,可得EF2=2CE2、 ∠ECF=∠ACB=90°、∠CEF=∠CFE=45°;再证明△ACE≌△CFB,可得AE=BF;然后再证FEB=90°,即∠BCE=135°;作△CEB的外接圆,圆心为O,取圆上任意一定G,连接BO、CO、BG、CG,根据四边形的外接圆的性质可得∠CGB=45°,∠COB=90°;再求得OB的长,最后运用弧长公式解答即可.
解:如图:过C作CF⊥CE且CE=CF
∴EF2=2CE2,∠ECF=∠ACB=90°,∠CEF=∠CFE=45°
∵∠ACE=∠ACB-∠ECB, ∠BCF=∠ECF-∠ECB,
∴∠ACE=∠BCF
∵在△ACE和△CFB中,AC=BC, ∠ACE=∠BCF,CE=CF
∴△ACE≌△CFB
∴AE=BF
∵AE2=BE2+2CE2
∴AE2=BE2+EF2
∴BF2=BE2+EF2,即∠FEB=90°
∴∠BCE=∠CEF+∠FEB=135°
如图:作△CEB的外接圆,圆心为O,取圆上任意一定G,连接BO、CO、BG、CG
则⊙O是四边形CEBG的外接圆
∴∠CGB=180°-∠BCE =45°
∴∠COB=90°
∵BC=4,OB=OC
∴OB=2![]()
∴![]() =
=![]() =
=![]()
故答案为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】把一张宽为1cm的长方形纸片ABCD折叠成如图所示的阴影图案,顶点A,D互相重合,中间空白部分是以E为直角顶点,腰长为2cm的等腰直角三角形,则纸片的长AD(单位:cm)为( )
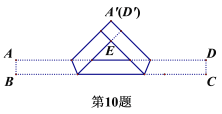
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
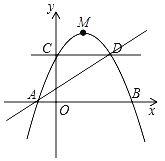
【题目】如图,已知顶点为M(![]() ,
,![]() )的抛物线过点D(3,2),交x轴于A,B两点,交y轴于点C,点P是抛物线上一动点.
)的抛物线过点D(3,2),交x轴于A,B两点,交y轴于点C,点P是抛物线上一动点.
(1)求抛物线的解析式;
(2)当点P在直线AD上方时,求△PAD面积的最大值,并求出此时点P的坐标;
(3)过点P作直线CD的垂线,垂足为Q,若将△CPQ沿CP翻折,点Q的对应点为Q'.是否存在点P,使Q'恰好落在x轴上?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年端午节期间,小华都要自制 A、B 两种类型的粽子在线上线下进行销售,今年他经过市场调查发现,若制作 3 个 A 型粽子 2 个 B 型粽子需成本 11 元,若制作 2 个 A 型粽子 3 个B 型粽子需成本 11.5 元.
(1)求今年制作 A、B 两种类型的粽子每个的成本分别是多少元?
(2)由于今年的疫情,小华预计网上销售会大增,所以决定制作 A 型粽子 2000 个,B 型粽子 1000 个,并且统一售价每个 4 元,销售一段时间后,随着端午节的临近,小华把剩余的粽子打 8 折全部通过线上线下两种方式售出,在制作和销售过程中还产生了除成本以外其它费用合计 700 元,小华在这次买卖中赚到至少 4000 元,则打折销售的粽子最多是多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了庆祝中华人民共和国成立70周年,某市决定开展“我和祖国共成长”主题演讲比赛,某中学将参加本校选拔赛的40名选手的成绩(满分为100分,得分为正整数且无满分,最低为75分)分成五组,并绘制了下列不完整的统计图表.
分数段 | 频数 | 频率 |
74.5~79.5 | 2 | 0.05 |
79.5~84.5 | m | 0.2 |
84.5~89.5 | 12 | 0.3 |
89.5~94.5 | 14 | n |
94.5~99.5 | 4 | 0.1 |
(1)表中m=__________,n=____________;
(2)请在图中补全频数直方图;
(3)甲同学的比赛成绩是40位参赛选手成绩的中位数,据此推测他的成绩落在_________分数段内;
(4)选拔赛中,成绩在94.5分以上的选手,男生和女生各占一半,学校从中随机确定2名选手参加全市决赛,请用列举法或树状图法求恰好是一名男生和一名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
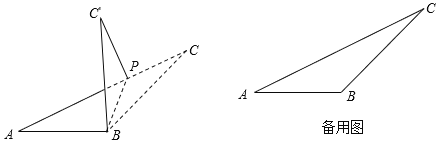
【题目】已知:如图,∠ABC=135°,AB=a,BC=b,点P是边AC上任意一点,连结BP,将△CPB沿PB翻折,得△C'PB.
(1)若a=![]() ,b=6,∠C'PC=90°,求CP的长;
,b=6,∠C'PC=90°,求CP的长;
(2)连结AC',当以A、B、P、C'为顶点的四边形是平行四边形时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲,乙两个电子团队整理一批电脑数据,整理电脑的台数为![]() (台)与整理需要的时间
(台)与整理需要的时间![]() 之间关系如下图所示,请依据图象提供的信息解答下列问题:
之间关系如下图所示,请依据图象提供的信息解答下列问题:
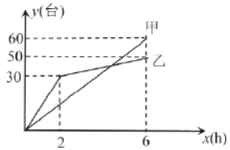
(1)乙队工作![]() 小时整理_____台电脑,工作
小时整理_____台电脑,工作![]() 时两队一共整理了_______台;
时两队一共整理了_______台;
(2)求甲、乙两队![]() 与
与![]() 的关系式.
的关系式.
(3)甲、乙两队整理电脑台数相等时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
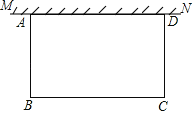
【题目】如图,在足够大的空地上有一段长为a(a≥50)米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
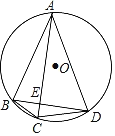
【题目】如图,四边形ABCD内接于⊙O,AC⊥BD于E.
(1)用尺规作图作DF⊥AB于F,交AC于G,并标出F、G(保留作图痕迹,不写作法);
(2)在(1)中,若∠BAD=45°,求证:EG=EC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com