
【题目】每年端午节期间,小华都要自制 A、B 两种类型的粽子在线上线下进行销售,今年他经过市场调查发现,若制作 3 个 A 型粽子 2 个 B 型粽子需成本 11 元,若制作 2 个 A 型粽子 3 个B 型粽子需成本 11.5 元.
(1)求今年制作 A、B 两种类型的粽子每个的成本分别是多少元?
(2)由于今年的疫情,小华预计网上销售会大增,所以决定制作 A 型粽子 2000 个,B 型粽子 1000 个,并且统一售价每个 4 元,销售一段时间后,随着端午节的临近,小华把剩余的粽子打 8 折全部通过线上线下两种方式售出,在制作和销售过程中还产生了除成本以外其它费用合计 700 元,小华在这次买卖中赚到至少 4000 元,则打折销售的粽子最多是多少个?
【答案】(1)制作A型粽子每个的成本是2元,B型粽子每个的成本是2.5元;(2)打折销售的粽子最多是1000个.
【解析】
(1)设制作A型粽子每个的成本是![]() 元,B型粽子每个的成本是
元,B型粽子每个的成本是![]() 元,然后根据“制作 3 个 A 型粽子 2 个 B 型粽子需成本 11 元,若制作 2 个 A 型粽子 3 个B 型粽子需成本 11.5 元”列出二元一次方程组即可求出结论;
元,然后根据“制作 3 个 A 型粽子 2 个 B 型粽子需成本 11 元,若制作 2 个 A 型粽子 3 个B 型粽子需成本 11.5 元”列出二元一次方程组即可求出结论;
(2)设打折销售的粽子是![]() 个,根据题意,列出一元一次不等式即可求出结论.
个,根据题意,列出一元一次不等式即可求出结论.
(1)解:设制作A型粽子每个的成本是![]() 元,B型粽子每个的成本是
元,B型粽子每个的成本是![]() 元,
元,
![]()
解得:![]()
答:制作A型粽子每个的成本是2元,B型粽子每个的成本是2.5元.
(2)解:设打折销售的粽子是![]() 个
个
![]()
解得:![]()
答:打折销售的粽子最多是1000个.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 和
和![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
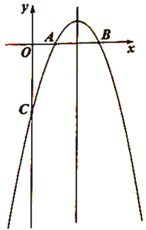
(1)求该抛物线的解析式;
(2)绕点![]() 旋转的直线
旋转的直线![]() :
:![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与抛物线相交于点
,与抛物线相交于点![]() ,且满足
,且满足![]() 时,求直线
时,求直线![]() 的解析式;
的解析式;
(3)点![]() 为抛物线上的一点,点
为抛物线上的一点,点![]() 为抛物线对称轴上的一点,是否存在以点
为抛物线对称轴上的一点,是否存在以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的平行四边形,若存在,请直接写出点
为顶点的平行四边形,若存在,请直接写出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
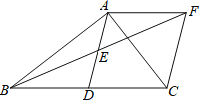
【题目】如图,在![]() ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:![]() AEF≌△DEB;
AEF≌△DEB;
(2)若∠BAC=90°,求证:四边形ADCF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.

(1)求证:四边形BFDE为平行四边形;
(2)若四边形BFDE为菱形,且AB=2,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】港口 A、B、C 依次在同一条直线上,甲、乙两艘船同时分别从 A、B两港出发,匀速驶向 C 港,甲、乙两船与 B 港的距离 y(海里)与行驶时间 x 时)之间的函数关系如图所示,则下列说法错误的是( )
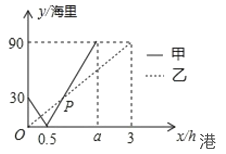
A.甲船平均速度为 60 海里/时B.乙船平均速度为 30 海里/时
C.甲、乙两船在途中相遇两次D.A、C 两港之间的距离为 120 海里
查看答案和解析>>
科目:初中数学 来源: 题型:
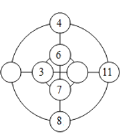
【题目】2017年,随州学子尤东梅参加《最强大脑》节目,成功完成了高难度的项目挑战,展现了惊人的记忆力.在2019年的《最强大脑》节目中,也有很多具有挑战性的比赛项目,其中《幻圆》这个项目充分体现了数学的魅力.如图是一个最简单的二阶幻圆的模型,要求:①内、外两个圆周上的四个数字之和相等;②外圆两直径上的四个数字之和相等,则图中两空白圆圈内应填写的数字之和为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,已知∠ACB=90°,AC=BC=4,若点E在△ABC内部运动,且满足AE2=BE2+2CE2,则点E的运动路径长是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图反映了我国2014-2019年快递业务量(位:亿件)及年增长率(%)的情况
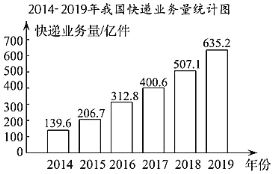
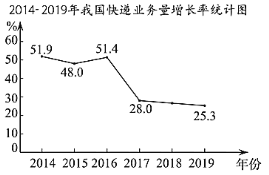
(以上数据来源于国家统计局网站)
根据统计图提供的信息,下列推断不合理的是( )
A.2014-2019年,我国快递业务量的年平均值超过300亿件
B.与2017年相比,2018年我国快递业务量的增长率超过25%
C.2014-2019年,我国快递业务量与年增长率都是逐年增长
D.2019年我国的快递业务量比2014年的4倍还多
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (
(![]() 是常数,
是常数,![]() )与
)与![]() 轴交于
轴交于![]() 两点,顶点
两点,顶点![]() 给出下列结论:①
给出下列结论:①![]() ;②若
;②若![]() 在抛物线上,则
在抛物线上,则![]() ;③关于
;③关于![]() 的方程
的方程![]() 有实数解,则
有实数解,则![]() ;④当
;④当![]() 时,
时,![]() 为等腰直角三角形,其中正确的结论是( )
为等腰直角三角形,其中正确的结论是( )
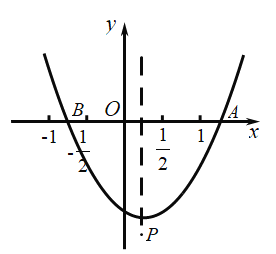
A.①②B.①③C.②③D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com