
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 和
和![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
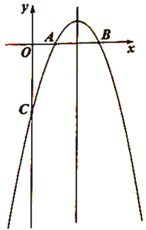
(1)求该抛物线的解析式;
(2)绕点![]() 旋转的直线
旋转的直线![]() :
:![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与抛物线相交于点
,与抛物线相交于点![]() ,且满足
,且满足![]() 时,求直线
时,求直线![]() 的解析式;
的解析式;
(3)点![]() 为抛物线上的一点,点
为抛物线上的一点,点![]() 为抛物线对称轴上的一点,是否存在以点
为抛物线对称轴上的一点,是否存在以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的平行四边形,若存在,请直接写出点
为顶点的平行四边形,若存在,请直接写出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
【答案】(1)抛物线的解析式为:![]() ;(2)直线
;(2)直线![]() 的解析式为
的解析式为![]() 或
或![]() ;(3)存在,符合题意的点
;(3)存在,符合题意的点![]() 有3个:
有3个:![]() ,
,![]() ,
,![]()
【解析】
(1把![]() 和
和![]() 代入
代入![]() 中得到一个关于a,b的二元一次方程组,把这个方程组解出来即可;
中得到一个关于a,b的二元一次方程组,把这个方程组解出来即可;
(2)分两种情况讨论进行计算即可;
(3)分三种情况讨论,利用平行四边形的性质列方程求解即可.
解:(1)∵抛物线经过点![]() ,点
,点![]() ,
,
∴![]() 解得:
解得:![]()
∴抛物线的解析式为:![]()
(2)①如图1,当点![]() 、
、![]() 在点
在点![]() 的异侧时,过点
的异侧时,过点![]() 作
作![]() 轴于点
轴于点![]()
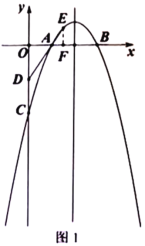
∴![]()
∵![]()
∴![]() ,
,
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴点![]() 与点
与点![]() 的横坐标为
的横坐标为![]()
∴点![]() 的纵坐标为
的纵坐标为![]()
![]() ∴点
∴点![]() 的坐标为
的坐标为![]()
∵直线![]() :
:![]() 过点
过点![]() 和点
和点![]()
∴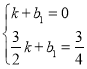 解得:
解得: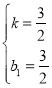
∴直线![]() 的解析式为
的解析式为![]()
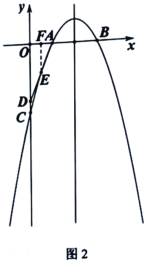
②如图2,当点![]() 、
、![]() 在点
在点![]() 的同侧时,过点
的同侧时,过点![]() 作
作![]() 轴于点
轴于点![]()
∴![]()
∵![]()
∴![]() ,
,
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴点![]() 与点
与点![]() 的横坐标为
的横坐标为![]()
∴点![]() 的纵坐标为
的纵坐标为![]()
∴点![]() 的坐标为
的坐标为![]()
∵直线![]() :
:![]() 过点
过点![]() 和点
和点![]()
∴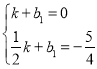 解得:
解得: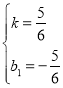
∴直线![]() 的解析式为
的解析式为![]()
综上所述:直线![]() 的解析式为
的解析式为![]() 或
或![]() .
.
(3)存在,符合题意的点![]() 有3个它们分别是:
有3个它们分别是:![]() ,
,![]() ,
,![]() .
.
设P的坐标为P(x, ![]() ),点Q的坐标为(2,y)
),点Q的坐标为(2,y)
当BP∥CQ时,则![]() ,解得x=1,
,解得x=1,
∴![]() =
=![]()
∴![]() .
.
当BP∥QC时,则![]() ,解得x=5,
,解得x=5,
∴![]() =
=![]()
∴![]() ,
,
③当BC∥PQ时,则![]() ,解得x=-1,
,解得x=-1,
∴![]() =
=![]()
∴![]() .
.
综上所述,点![]() 有3个它们分别是:
有3个它们分别是:![]() ,
,![]() ,
,![]() .
.
【点晴】
本题考查了二次函数的综合应用,合理利用数形结合和分类讨论是解题的关键.


科目:初中数学 来源: 题型:
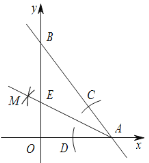
【题目】如图,直线y![]() x4与 x轴、y轴的交点为A,B.按以下步骤作图:
x4与 x轴、y轴的交点为A,B.按以下步骤作图:
①以点 A 为圆心,适当长度为半径作弧,分别交 AB,x 轴于点 C,D;
②分别以点 C,D 为圆心,大于![]() CD的长为半径作弧,两弧在∠OAB内交于点M;③作射线AM,交 y 轴于点E.则点 E 的坐标为____________
CD的长为半径作弧,两弧在∠OAB内交于点M;③作射线AM,交 y 轴于点E.则点 E 的坐标为____________
查看答案和解析>>
科目:初中数学 来源: 题型:
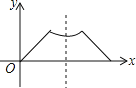
【题目】已知点P为某个封闭图形边界上的一定点,动点M从点P出发,沿其边界顺时针匀速运动一周,设点M的运动时间为x,线段PM的长度为y,表示y与x的函数图象大致如图所示,则该封闭图形可能是( )
A. 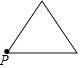 B.
B.  C.
C. 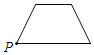 D.
D. 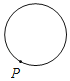
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金秋时节,硕果飘香,某精准扶贫项目果园上市一种有机生态水果.为帮助果园拓宽销路,欣欣超市对这种水果进行代销,进价为5元/千克,售价为6元/千克时,当天的销售量为100千克;在销售过程中发现:销售单价每上涨0.5元,当天的销售量就减少5千克.设当天销售单价统一为x元/千克(x≥6,且x是按0.5元的倍数上涨),当天销售利润为y元.
(1)求y与x的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价所在的范围;
(3)若该种水果每千克的利润不超过80%,要想当天获得利润最大,每千克售价为多少元?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行统计,结果如下表,并绘制了如下尚不完整的统计图,已知![]() ,
,![]() 两组发言的人数比为5:2,请结合图表中相关数据回答下列问题:
两组发言的人数比为5:2,请结合图表中相关数据回答下列问题:
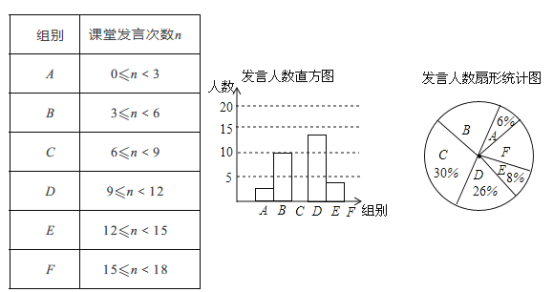
(1)本次抽样的学生人数为_________;
(2)补全条形统计图;
(3)该年级共有学生500人,请估计这天全年级发言次数不少于12的人数;
(4)已知![]() 组发言的学生中有1位女生,
组发言的学生中有1位女生,![]() 组发言的学生中有2位男生,现从
组发言的学生中有2位男生,现从![]() 组与
组与![]() 组中分别抽一位学生写报告,请用树状图或列表法,求所抽到的两位学生恰好是一男一女的概率.
组中分别抽一位学生写报告,请用树状图或列表法,求所抽到的两位学生恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
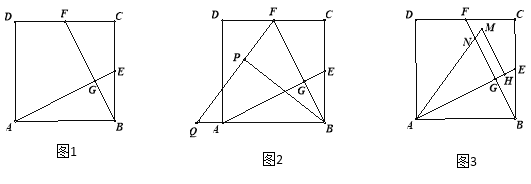
【题目】如图1,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF,交点为G.
(1)求证:AE⊥BF;
(2)将△BCF沿BF对折,得到△BPF(如图2),延长FP交BA的延长线于点Q,求sin∠BQP的值;
(3)将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,得到△AHM(如图3),若AM和BF相交于点N,当正方形ABCD的边长为4时,直接写出四边形GHMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
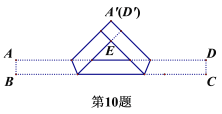
【题目】把一张宽为1cm的长方形纸片ABCD折叠成如图所示的阴影图案,顶点A,D互相重合,中间空白部分是以E为直角顶点,腰长为2cm的等腰直角三角形,则纸片的长AD(单位:cm)为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
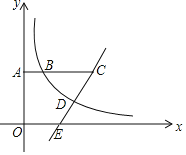
【题目】如图,已知点![]() ,
,![]() ,且点B在双曲线
,且点B在双曲线![]() 上,在AB的延长线上取一点C,过点C的直线交双曲线于点D,交x轴正半轴于点E,且
上,在AB的延长线上取一点C,过点C的直线交双曲线于点D,交x轴正半轴于点E,且![]() ,则线段CE长度的取值范围是
,则线段CE长度的取值范围是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年端午节期间,小华都要自制 A、B 两种类型的粽子在线上线下进行销售,今年他经过市场调查发现,若制作 3 个 A 型粽子 2 个 B 型粽子需成本 11 元,若制作 2 个 A 型粽子 3 个B 型粽子需成本 11.5 元.
(1)求今年制作 A、B 两种类型的粽子每个的成本分别是多少元?
(2)由于今年的疫情,小华预计网上销售会大增,所以决定制作 A 型粽子 2000 个,B 型粽子 1000 个,并且统一售价每个 4 元,销售一段时间后,随着端午节的临近,小华把剩余的粽子打 8 折全部通过线上线下两种方式售出,在制作和销售过程中还产生了除成本以外其它费用合计 700 元,小华在这次买卖中赚到至少 4000 元,则打折销售的粽子最多是多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com