练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

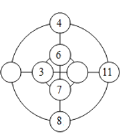
    【题目】2017年，随州学子尤东梅参加《最强大脑》节目，成功完成了高难度的项目挑战，展现了惊人的记忆力．在2019年的《最强大脑》节目中，也有很多具有挑战性的比赛项目，其中《幻圆》这个项目充分体现了数学的魅力．如图是一个最简单的二阶幻圆的模型，要求：①内、外两个圆周上的四个数字之和相等；②外圆两直径上的四个数字之和相等，则图中两空白圆圈内应填写的数字之和为_____．

    【答案】11

    【解析】

    根据题意要求①②可得关于所要求的两数的两个等式，解出两数即可．

    解：设图中两空白圆圈内应填写的数字从左到右依次为a，b

    ∵外圆两直径上的四个数字之和相等

    ∴4+6+7+8=a+3+b+11①

    ∵内、外两个圆周上的四个数字之和相等

    ∴3+6+b+7=a+4+11+8②

    联立①②解得：

    a=2，b=9

    ∴图中两空白圆圈内应填写的数字从左到右依次为2，9

    2+9=11

    故答案为：11．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

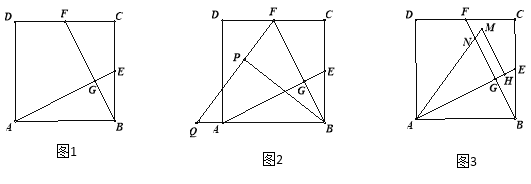
    【题目】如图1，在正方形ABCD中，E、F分别为BC、CD的中点，连接AE、BF，交点为G．

    (1)求证：AE⊥BF；

    (2)将△BCF沿BF对折，得到△BPF（如图2），延长FP交BA的延长线于点Q，求sin∠BQP的值；

    (3)将△ABE绕点A逆时针方向旋转，使边AB正好落在AE上，得到△AHM（如图3），若AM和BF相交于点N，当正方形ABCD的边长为4时，直接写出四边形GHMN的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

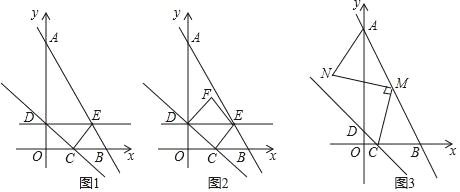
    【题目】已知，A（0，8），B（4，0），直线y＝﹣x沿x轴作平移运动，平移时交OA于D，交OB于C．

    （1）当直线y＝﹣x从点O出发以1单位长度/s的速度匀速沿x轴正方向平移，平移到达点B时结束运动，过点D作DE⊥y轴交AB于点E，连接CE，设运动时间为t（s）．

    ①是否存在t值，使得△CDE是以CD为腰的等腰三角形？如果能，请直接写出相应的t值；如果不能，请说明理由．

    ②将△CDE沿DE翻折后得到△FDE，设△EDF与△ADE重叠部分的面积为y（单位长度的平方）．求y关于t的函数关系式及相应的t的取值范围；

    （2）若点M是AB的中点，将MC绕点M顺时针旋转90°得到MN，连接AN，请直接写出AN+MN的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

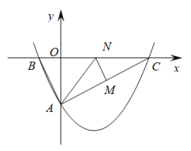
    【题目】如图，二次函数的图象与y轴交于点A(0，-4)，与x轴交于点B(-2，0)，C(8，0)，连接AB，AC．

    （1）求出二次函数表达式；

    （2）若点N在线段BC上运动（不与点B，C重合），过点N作NM∥AB，交AC于点M，连接AN，当以点A，M，N为顶点的三角形与以点A，B，O为顶点的三角形相似时，求此时点N的坐标；

    （3）若点N在x轴上运动，当以点A，N，C为顶点的三角形是等腰三角形时，请直接写出此时点N的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】每年端午节期间，小华都要自制 A、B 两种类型的粽子在线上线下进行销售，今年他经过市场调查发现，若制作 3 个 A 型粽子 2 个 B 型粽子需成本 11 元，若制作 2 个 A 型粽子 3 个B 型粽子需成本 11.5 元．

    (1)求今年制作 A、B 两种类型的粽子每个的成本分别是多少元？

    (2)由于今年的疫情，小华预计网上销售会大增，所以决定制作 A 型粽子 2000 个，B 型粽子 1000 个，并且统一售价每个 4 元，销售一段时间后，随着端午节的临近，小华把剩余的粽子打 8 折全部通过线上线下两种方式售出，在制作和销售过程中还产生了除成本以外其它费用合计 700 元，小华在这次买卖中赚到至少 4000 元，则打折销售的粽子最多是多少个？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在平面直角坐标系中，点O为坐标原点，抛物线y＝ax2+bx+c与y轴交于点A（0，6），与x轴交于点B（﹣2，0），C（6，0）．

    （1）直接写出抛物线的解析式及其对称轴；

    （2）如图2，连接AB，AC，设点P（m，n）是抛物线上位于第一象限内的一动点，且在对称轴右侧，过点P作PD⊥AC于点E，交x轴于点D，过点P作PG∥AB交AC于点F，交x轴于点G．设线段DG的长为d，求d与m的函数关系式，并注明m的取值范围；

    （3）在（2）的条件下，若△PDG的面积为，

    ①求点P的坐标；

    ②设M为直线AP上一动点，连接OM交直线AC于点S，则点M在运动过程中，在抛物线上是否存在点R，使得△ARS为等腰直角三角形？若存在，请直接写出点M及其对应的点R的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

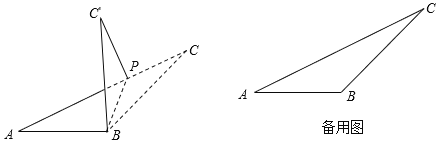
    【题目】已知：如图，∠ABC＝135°，AB＝a，BC＝b，点P是边AC上任意一点，连结BP，将△CPB沿PB翻折，得△C'PB．

    （1）若a＝，b＝6，∠C'PC＝90°，求CP的长；

    （2）连结AC'，当以A、B、P、C'为顶点的四边形是平行四边形时，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

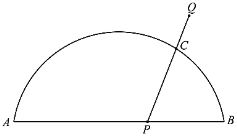
    【题目】如图，是与弦所围成图形的外部的一定点，是弦上的一动点，连接交于点．已知，设，两点间的距离为，，两点间的距离为，，两点间的距离为．

    小石根据学习函数的经验，分别对函数，随自变量的变化而变化的规律进行了探究，下面是小石的探究过程，请补充完整：

    （1）按照下表中自变量的值进行取点、画图、测量分别得到了，与的几组对应值：

    0

    1

    2

    3

    4

    5

    5.40

    6

    4.63

    3.89

    2.61

    2.15

    1.79

    1.63

    0.95

    1.20

    1.11

    1.04

    0.99

    1.02

    1.21

    1.40

    2.21

    （2）在同一平面直角坐标系中，描出补全后的表中各组数值所对应的点，，并画出函数，的图象；

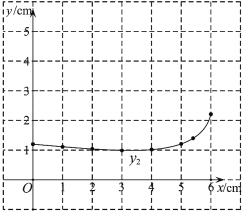
    （3）结合函数图象，解决问题：当为的中点时，的长度约为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：

    我们知道，四边形的一条对角线把这个四边形分成了两个三角形，如果这两个三角形相似（不全等），我们就把这条对角线叫做这个四边形的“相似对角线”．

    理解：

    （1）如图1，已知Rt△ABC在正方形网格中，请你只用无刻度的直尺在网格中找到一点D，使四边形ABCD是以AC为“相似对角线”的四边形（保留画图痕迹，找出3个即可）；

    （2）如图2，在四边形ABCD中，∠ABC=80°，∠ADC=140°，对角线BD平分∠ABC．

    求证：BD是四边形ABCD的“相似对角线”；

    （3）如图3，已知FH是四边形EFCH的“相似对角线”，∠EFH=∠HFG=30°，连接EG，若△EFG的面积为2，求FH的长．

    查看答案和解析>>

    同步练习册答案