
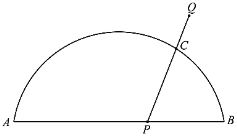
【题目】如图,![]() 是
是![]() 与弦
与弦![]() 所围成图形的外部的一定点,
所围成图形的外部的一定点,![]() 是弦
是弦![]() 上的一动点,连接
上的一动点,连接![]() 交
交![]() 于点
于点![]() .已知
.已知![]() ,设
,设![]() ,
,![]() 两点间的距离为
两点间的距离为![]() ,
,![]() ,
,![]() 两点间的距离为
两点间的距离为![]() ,
,![]() ,
,![]() 两点间的距离为
两点间的距离为![]() .
.
小石根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
(1)按照下表中自变量![]() 的值进行取点、画图、测量分别得到了
的值进行取点、画图、测量分别得到了![]() ,
,![]() 与
与![]() 的几组对应值:
的几组对应值:
| 0 | 1 | 2 | 3 | 4 | 5 | 5.40 | 6 |
| 4.63 | 3.89 | 2.61 | 2.15 | 1.79 | 1.63 | 0.95 | |
| 1.20 | 1.11 | 1.04 | 0.99 | 1.02 | 1.21 | 1.40 | 2.21 |
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() ,
,![]() 的图象;
的图象;
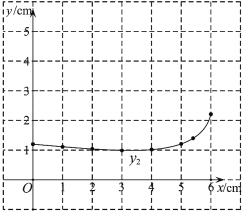
(3)结合函数图象,解决问题:当![]() 为
为![]() 的中点时,
的中点时,![]() 的长度约为______
的长度约为______![]() .
.
科目:初中数学 来源: 题型:
【题目】如图,从左向右依次摆放序号分别为1,2,3,…,n的小桶,其中任意相邻的四个小桶所放置的小球个数之和相等.
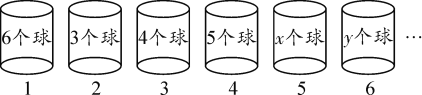
尝试 求x+y的值;
应用 若n=22,则这些小桶内所放置的小球个数之和是多少?
发现 用含k(k为正整数)的代数式表示装有“4个球”的小桶序号.
查看答案和解析>>
科目:初中数学 来源: 题型:
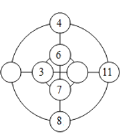
【题目】2017年,随州学子尤东梅参加《最强大脑》节目,成功完成了高难度的项目挑战,展现了惊人的记忆力.在2019年的《最强大脑》节目中,也有很多具有挑战性的比赛项目,其中《幻圆》这个项目充分体现了数学的魅力.如图是一个最简单的二阶幻圆的模型,要求:①内、外两个圆周上的四个数字之和相等;②外圆两直径上的四个数字之和相等,则图中两空白圆圈内应填写的数字之和为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中放入![]() 个大小形状几乎完全相同实验用的鸡蛋,鸡蛋的质量有微小的差距(用手感觉不到差异),质量分别为
个大小形状几乎完全相同实验用的鸡蛋,鸡蛋的质量有微小的差距(用手感觉不到差异),质量分别为![]() 、
、![]() 、
、![]() 克,已知随机的摸出一个鸡蛋,摸到
克,已知随机的摸出一个鸡蛋,摸到![]() 克和
克和![]() 克的鸡蛋的概率是相等的.
克的鸡蛋的概率是相等的.
(1)求这四个鸡蛋质量的众数和中位数
(2)小明做实验需要拿走一个鸡蛋,芳芳在小明拿走后从剩下的三个鸡蛋中随机的拿走一个
①通过计算分析小明拿走一个鸡蛋后,剩下的三个鸡蛋质量的中位数是多少?
②假设小明拿走的鸡蛋质量为![]() 克,芳芳随机的拿出一个鸡蛋后又放回,之后再随机的拿出一个鸡蛋,请用树状图求芳芳两次拿到都是
克,芳芳随机的拿出一个鸡蛋后又放回,之后再随机的拿出一个鸡蛋,请用树状图求芳芳两次拿到都是![]() 克的鸡蛋的概率?
克的鸡蛋的概率?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图反映了我国2014-2019年快递业务量(位:亿件)及年增长率(%)的情况
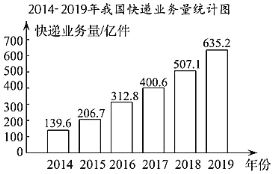
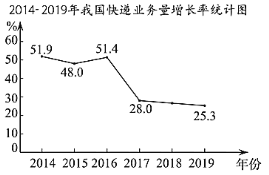
(以上数据来源于国家统计局网站)
根据统计图提供的信息,下列推断不合理的是( )
A.2014-2019年,我国快递业务量的年平均值超过300亿件
B.与2017年相比,2018年我国快递业务量的增长率超过25%
C.2014-2019年,我国快递业务量与年增长率都是逐年增长
D.2019年我国的快递业务量比2014年的4倍还多
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,...都是等腰直角三角形,其直角顶点
,...都是等腰直角三角形,其直角顶点![]() ,
,![]() ,
,![]() ,...均在直线
,...均在直线![]() 上,设
上,设![]() ,
,![]() ,
,![]() ,...的面积分别为
,...的面积分别为![]() ,
,![]() ,
,![]() ,...,依据图形所反映的规律,S2020=__________.
,...,依据图形所反映的规律,S2020=__________.
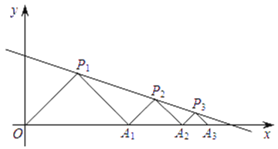
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,在图中按下列步骤进行尺规作图:
,在图中按下列步骤进行尺规作图:
① | 以 |
② | 分别以 |
③ | 画射线 |
下列说法错误的是( )
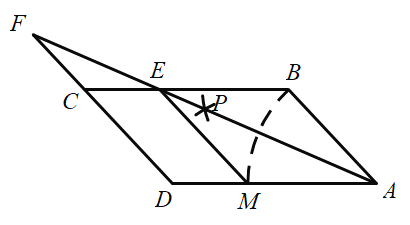
A.![]() B.
B.![]()
C.![]() D.若
D.若![]() ,则
,则![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球队员在篮球联赛中分别与甲队、乙队对阵各四场,下表是他的技术统计.
场次 | 对阵甲队 | 对阵乙队 | ||
得分(分) | 失误(次) | 得分(分) | 失误(次) | |
第一场 | 25 | 2 | 27 | 3 |
第二场 | 30 | 0 | 31 | 1 |
第三场 | 27 | 3 | 20 | 2 |
第四场 | 26 | 2 | 26 | 4 |
(1)他在对阵甲队和乙队的各四场比赛中,平均每场得分分别是多少?
(2)利用方差判断他在对阵哪个队时得分比较稳定;
(3)根据上表提供的信息,判断他在对阵哪个队时总体发挥较好,简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
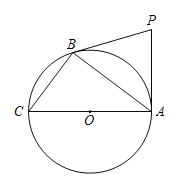
【题目】如图,PA,PB是⊙O的两条切线,A,B是切点,AC是⊙O的直径.
(1)若∠ACB=70°,求∠APB的度数;
(2)连接OP,若AB=8,BC=6,求OP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com