
【题目】如图,从左向右依次摆放序号分别为1,2,3,…,n的小桶,其中任意相邻的四个小桶所放置的小球个数之和相等.
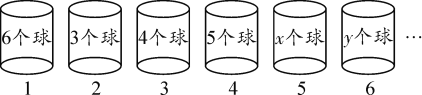
尝试 求x+y的值;
应用 若n=22,则这些小桶内所放置的小球个数之和是多少?
发现 用含k(k为正整数)的代数式表示装有“4个球”的小桶序号.
【答案】尝试:x+y=9;应用:99;发现:装有“4个球”的小桶序号为4k-1.
【解析】
尝试:根据“任意相邻的四个小桶所放置的小球个数之和相等”列出等式即可得到x+y的值;
应用:根据题意可分别求出x,y的值,可以发现以“6,3,4,5”为一组循环出现,故可求出n=22时,小桶内所放置的小球个数之和;
发现:根据规律,用含有k的代数式表示即可.
尝试:根据题意可得6+3+4+5=4+5+x+y,
∴x+y=9;
应用:∵6+3+4+5=3+4+5+x,
又∵x+y=9,
∴x=6,y=3,
∴小桶内所放置的小球数每四个一循环,
∵22÷4=52,
∴(6+3+4+5)×5+9=99
发现:装有“4个球”的小桶序号分别为3=4×1-1,7=4×2-1,11=4×3-1…,
∴装有“4个球”的小桶序号为4k-1.


科目:初中数学 来源: 题型:
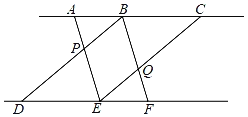
【题目】如图,已知AC∥DF,点B在AC上,点E在DF上,连结AE,BD相交于点P,连结CE,BF相交于点Q,若AB=EF,BC=DE.
(1)求证:四边形BPEQ为平行四边形;
(2)若DP=2BP,BF=3,CE=6.求证:四边形BPEQ为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
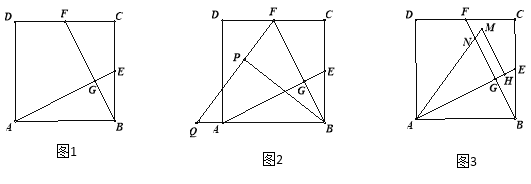
【题目】如图1,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF,交点为G.
(1)求证:AE⊥BF;
(2)将△BCF沿BF对折,得到△BPF(如图2),延长FP交BA的延长线于点Q,求sin∠BQP的值;
(3)将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,得到△AHM(如图3),若AM和BF相交于点N,当正方形ABCD的边长为4时,直接写出四边形GHMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
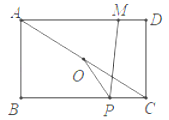
【题目】如图,在矩形ABCD中,AB=4,AD=5,连接AC,O是AC的中点,M是AD上一点,且MD=1,P是BC上一动点,则PM﹣PO的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
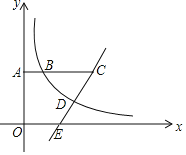
【题目】如图,已知点![]() ,
,![]() ,且点B在双曲线
,且点B在双曲线![]() 上,在AB的延长线上取一点C,过点C的直线交双曲线于点D,交x轴正半轴于点E,且
上,在AB的延长线上取一点C,过点C的直线交双曲线于点D,交x轴正半轴于点E,且![]() ,则线段CE长度的取值范围是
,则线段CE长度的取值范围是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
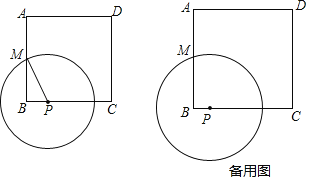
【题目】如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.
(1)当BP= 时,△MBP~△DCP;
(2)当⊙P与正方形ABCD的边相切时,求BP的长;
(3)设⊙P的半径为x,请直接写出正方形ABCD中恰好有两个顶点在圆内的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
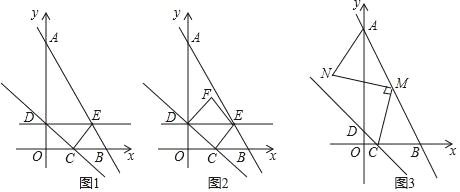
【题目】已知,A(0,8),B(4,0),直线y=﹣x沿x轴作平移运动,平移时交OA于D,交OB于C.
(1)当直线y=﹣x从点O出发以1单位长度/s的速度匀速沿x轴正方向平移,平移到达点B时结束运动,过点D作DE⊥y轴交AB于点E,连接CE,设运动时间为t(s).
①是否存在t值,使得△CDE是以CD为腰的等腰三角形?如果能,请直接写出相应的t值;如果不能,请说明理由.
②将△CDE沿DE翻折后得到△FDE,设△EDF与△ADE重叠部分的面积为y(单位长度的平方).求y关于t的函数关系式及相应的t的取值范围;
(2)若点M是AB的中点,将MC绕点M顺时针旋转90°得到MN,连接AN,请直接写出AN+MN的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
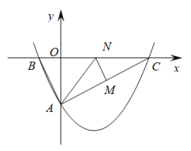
【题目】如图,二次函数![]() 的图象与y轴交于点A(0,-4),与x轴交于点B(-2,0),C(8,0),连接AB,AC.
的图象与y轴交于点A(0,-4),与x轴交于点B(-2,0),C(8,0),连接AB,AC.
(1)求出二次函数表达式;
(2)若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AB,交AC于点M,连接AN,当以点A,M,N为顶点的三角形与以点A,B,O为顶点的三角形相似时,求此时点N的坐标;
(3)若点N在x轴上运动,当以点A,N,C为顶点的三角形是等腰三角形时,请直接写出此时点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
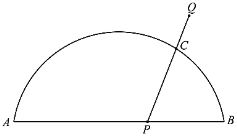
【题目】如图,![]() 是
是![]() 与弦
与弦![]() 所围成图形的外部的一定点,
所围成图形的外部的一定点,![]() 是弦
是弦![]() 上的一动点,连接
上的一动点,连接![]() 交
交![]() 于点
于点![]() .已知
.已知![]() ,设
,设![]() ,
,![]() 两点间的距离为
两点间的距离为![]() ,
,![]() ,
,![]() 两点间的距离为
两点间的距离为![]() ,
,![]() ,
,![]() 两点间的距离为
两点间的距离为![]() .
.
小石根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
(1)按照下表中自变量![]() 的值进行取点、画图、测量分别得到了
的值进行取点、画图、测量分别得到了![]() ,
,![]() 与
与![]() 的几组对应值:
的几组对应值:
| 0 | 1 | 2 | 3 | 4 | 5 | 5.40 | 6 |
| 4.63 | 3.89 | 2.61 | 2.15 | 1.79 | 1.63 | 0.95 | |
| 1.20 | 1.11 | 1.04 | 0.99 | 1.02 | 1.21 | 1.40 | 2.21 |
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() ,
,![]() 的图象;
的图象;
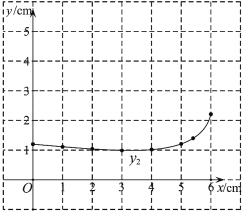
(3)结合函数图象,解决问题:当![]() 为
为![]() 的中点时,
的中点时,![]() 的长度约为______
的长度约为______![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com