
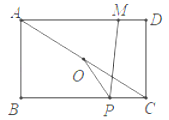
【题目】如图,在矩形ABCD中,AB=4,AD=5,连接AC,O是AC的中点,M是AD上一点,且MD=1,P是BC上一动点,则PM﹣PO的最大值为_____.
【答案】![]()
【解析】
连接MO并延长交BC于P,则此时,PMPO的值最大,且PMPO的最大值=OM,根据全等三角形的性质得到AM=CP=4,OM=OP,求得PB=1,过M作MN⊥BC于N,得到四边形MNCD是矩形,得到MN=CD,CN=DM,根据勾股定理即可得到结论.
∵在矩形ABCD中,AD=5,MD=1,
∴AM=AD﹣DM=5﹣1=4,
连接MO并延长交BC于P,
则此时,PM﹣PO的值最大,且PM﹣PO的最大值=OM,
∵AM∥CP,
∴∠MAO=∠PCO,
∵∠AOM=∠COP,AO=CO,
∴△AOM≌△COP(ASA),
∴AM=CP=4,OM=OP,
∴PB=5﹣4=1,
过M作MN⊥BC于N,
∴四边形MNCD是矩形,
∴MN=CD=AB=4,CN=DM=1,
∴PN=5﹣1﹣1=3,
∴MP=![]() ,
,
∴OM=![]() =
=![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在长方形 ABCD 中,放入六个形状大小相同的长方形,所标尺寸如图所示, 则图中阴影部分面积为( )

A. 44cm2B. 36cm2C. 96 cm2D. 84cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
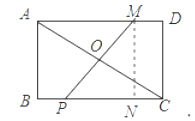
【题目】如图,在平面直角坐标系中,![]() ,以
,以![]() 为一边,在第一象限作菱形
为一边,在第一象限作菱形![]() ,并使
,并使![]() ,再以对角线
,再以对角线![]() 为一边,在如图所示的一侧作相同形状的菱形
为一边,在如图所示的一侧作相同形状的菱形![]() ,再依次作菱形
,再依次作菱形![]() ,
,![]() ,……,
,……,![]() ,则
,则![]() 的长度为_________.
的长度为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
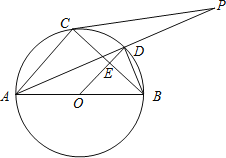
【题目】如图,⊙O是以AB为直径的△ABC的外接圆,点D是劣弧![]() 的中点,连结AD并延长,与过C点的直线交于P,OD与BC相交于点E.
的中点,连结AD并延长,与过C点的直线交于P,OD与BC相交于点E.
(1)求证:OE=![]() AC;
AC;
(2)连接CD,若∠PCD=∠PAC,试判断直线PC与⊙O的位置关系,并说明理由.
(3)在(2)的条件下,当AC=6,AB=10时,求切线PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠疫情期间,某校开展线上教学,有“录播”和“直播”两种教学方式供学生选择其中一种.为分析该校学生线上学习情况,在接受这两种教学方式的学生中各随机抽取40人调查学习参与度,数据整理结果如表(数据分组包含左端值不包含右端值).
参与度 人数 方式 | 0.2~0.4 | 0.4~0.6 | 0.6~0.8 | 0.8~1 |
录播 | 4 | 16 | 12 | 8 |
直播 | 2 | 10 | 16 | 12 |
(1)你认为哪种教学方式学生的参与度更高?简要说明理由.
(2)从教学方式为“直播”的学生中任意抽取一位学生,估计该学生的参与度在0.8及以上的概率是多少?
(3)该校共有800名学生,选择“录播”和“直播”的人数之比为1:3,估计参与度在0.4以下的共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中(如图),已知二次函数
中(如图),已知二次函数![]() (其中a、b、c是常数,且a≠0)的图像经过点A(0,-3)、B(1,0)、C(3,0),联结AB、AC.
(其中a、b、c是常数,且a≠0)的图像经过点A(0,-3)、B(1,0)、C(3,0),联结AB、AC.
(1)求这个二次函数的解析式;
(2)点D是线段AC上的一点,联结BD,如果![]() ,求tan∠DBC的值;
,求tan∠DBC的值;
(3)如果点E在该二次函数图像的对称轴上,当AC平分∠BAE时,求点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
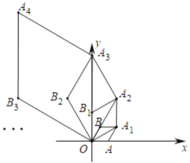
【题目】如图,从左向右依次摆放序号分别为1,2,3,…,n的小桶,其中任意相邻的四个小桶所放置的小球个数之和相等.
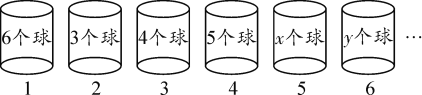
尝试 求x+y的值;
应用 若n=22,则这些小桶内所放置的小球个数之和是多少?
发现 用含k(k为正整数)的代数式表示装有“4个球”的小桶序号.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司用6000元购进A,B两种电话机25台,购买A种电话机与购买B种电话机的费用相等.已知A种电话机的单价是B种电话机单价的1.5倍.
(1)求A,B两种电话机的单价各是多少?
(2)若计划用不超过8000元的资金再次购进A,B两种话机共30台,已知A,B两种电话机的进价不变,求最多能购进多少台A种电话机?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中放入![]() 个大小形状几乎完全相同实验用的鸡蛋,鸡蛋的质量有微小的差距(用手感觉不到差异),质量分别为
个大小形状几乎完全相同实验用的鸡蛋,鸡蛋的质量有微小的差距(用手感觉不到差异),质量分别为![]() 、
、![]() 、
、![]() 克,已知随机的摸出一个鸡蛋,摸到
克,已知随机的摸出一个鸡蛋,摸到![]() 克和
克和![]() 克的鸡蛋的概率是相等的.
克的鸡蛋的概率是相等的.
(1)求这四个鸡蛋质量的众数和中位数
(2)小明做实验需要拿走一个鸡蛋,芳芳在小明拿走后从剩下的三个鸡蛋中随机的拿走一个
①通过计算分析小明拿走一个鸡蛋后,剩下的三个鸡蛋质量的中位数是多少?
②假设小明拿走的鸡蛋质量为![]() 克,芳芳随机的拿出一个鸡蛋后又放回,之后再随机的拿出一个鸡蛋,请用树状图求芳芳两次拿到都是
克,芳芳随机的拿出一个鸡蛋后又放回,之后再随机的拿出一个鸡蛋,请用树状图求芳芳两次拿到都是![]() 克的鸡蛋的概率?
克的鸡蛋的概率?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com