
【题目】新冠疫情期间,某校开展线上教学,有“录播”和“直播”两种教学方式供学生选择其中一种.为分析该校学生线上学习情况,在接受这两种教学方式的学生中各随机抽取40人调查学习参与度,数据整理结果如表(数据分组包含左端值不包含右端值).
参与度 人数 方式 | 0.2~0.4 | 0.4~0.6 | 0.6~0.8 | 0.8~1 |
录播 | 4 | 16 | 12 | 8 |
直播 | 2 | 10 | 16 | 12 |
(1)你认为哪种教学方式学生的参与度更高?简要说明理由.
(2)从教学方式为“直播”的学生中任意抽取一位学生,估计该学生的参与度在0.8及以上的概率是多少?
(3)该校共有800名学生,选择“录播”和“直播”的人数之比为1:3,估计参与度在0.4以下的共有多少人?
【答案】(1)“直播”教学方式学生的参与度更高,理由见解析;(2)30%;(3)50人
【解析】
(1)根据表格数据得出两种教学方式参与度在0.6以上的人数,比较即可作出判断;
(2)用表格中“直播”教学方式学生参与度在0.8以上的人数除以被调查的总人数即可估计对应概率;
(3)先根据“录播”和“直播”的人数之比为1:3及该校学生总人数求出“直播”、“录播”人数,再分别乘以两种教学方式中参与度在0.4以下人数所占比例求出对应人数,再相加即可得出答案.
解:(1)“直播”教学方式学生的参与度更高:
理由:“直播”参与度在0.6以上的人数为28人,“录播”参与度在0.6以上的人数为20人,参与度在0.6以上的“直播”人数远多于“录播”人数,
∴“直播”教学方式学生的参与度更高;
(2)12÷40=0.3=30%,
答:估计该学生的参与度在0.8及以上的概率是30%;
(3)“录播”总学生数为800×![]() =200(人),
=200(人),
“直播”总学生数为800×![]() =600(人),
=600(人),
∴“录播”参与度在0.4以下的学生数为200×![]() =20(人),
=20(人),
“直播”参与度在0.4以下的学生数为600×![]() =30(人),
=30(人),
∴参与度在0.4以下的学生共有20+30=50(人).


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】国庆70华诞期间,各超市购物市民络绎不绝,呈现浓浓节日气氛.“百姓超市”用320元购进一批葡萄,上市后很快脱销,该超市又用680元购进第二批葡萄,所购数量是第一批购进数量的2倍,但进价每市斤多了0.2元.
(1)该超市第一批购进这种葡萄多少市斤?
(2)如果这两次购进的葡萄售价相同,且全部售完后总利润不低于![]() ,那么每市斤葡萄的售价应该至少定为多少元?
,那么每市斤葡萄的售价应该至少定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金秋时节,硕果飘香,某精准扶贫项目果园上市一种有机生态水果.为帮助果园拓宽销路,欣欣超市对这种水果进行代销,进价为5元/千克,售价为6元/千克时,当天的销售量为100千克;在销售过程中发现:销售单价每上涨0.5元,当天的销售量就减少5千克.设当天销售单价统一为x元/千克(x≥6,且x是按0.5元的倍数上涨),当天销售利润为y元.
(1)求y与x的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价所在的范围;
(3)若该种水果每千克的利润不超过80%,要想当天获得利润最大,每千克售价为多少元?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
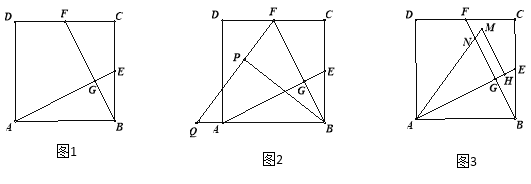
【题目】如图1,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF,交点为G.
(1)求证:AE⊥BF;
(2)将△BCF沿BF对折,得到△BPF(如图2),延长FP交BA的延长线于点Q,求sin∠BQP的值;
(3)将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,得到△AHM(如图3),若AM和BF相交于点N,当正方形ABCD的边长为4时,直接写出四边形GHMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
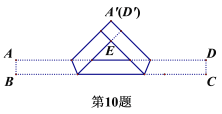
【题目】把一张宽为1cm的长方形纸片ABCD折叠成如图所示的阴影图案,顶点A,D互相重合,中间空白部分是以E为直角顶点,腰长为2cm的等腰直角三角形,则纸片的长AD(单位:cm)为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
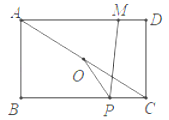
【题目】如图,在矩形ABCD中,AB=4,AD=5,连接AC,O是AC的中点,M是AD上一点,且MD=1,P是BC上一动点,则PM﹣PO的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
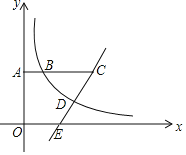
【题目】如图,已知点![]() ,
,![]() ,且点B在双曲线
,且点B在双曲线![]() 上,在AB的延长线上取一点C,过点C的直线交双曲线于点D,交x轴正半轴于点E,且
上,在AB的延长线上取一点C,过点C的直线交双曲线于点D,交x轴正半轴于点E,且![]() ,则线段CE长度的取值范围是
,则线段CE长度的取值范围是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
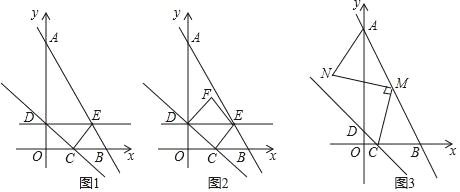
【题目】已知,A(0,8),B(4,0),直线y=﹣x沿x轴作平移运动,平移时交OA于D,交OB于C.
(1)当直线y=﹣x从点O出发以1单位长度/s的速度匀速沿x轴正方向平移,平移到达点B时结束运动,过点D作DE⊥y轴交AB于点E,连接CE,设运动时间为t(s).
①是否存在t值,使得△CDE是以CD为腰的等腰三角形?如果能,请直接写出相应的t值;如果不能,请说明理由.
②将△CDE沿DE翻折后得到△FDE,设△EDF与△ADE重叠部分的面积为y(单位长度的平方).求y关于t的函数关系式及相应的t的取值范围;
(2)若点M是AB的中点,将MC绕点M顺时针旋转90°得到MN,连接AN,请直接写出AN+MN的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
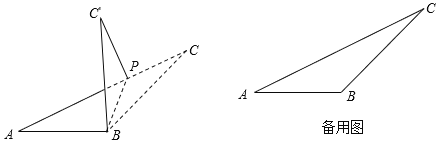
【题目】已知:如图,∠ABC=135°,AB=a,BC=b,点P是边AC上任意一点,连结BP,将△CPB沿PB翻折,得△C'PB.
(1)若a=![]() ,b=6,∠C'PC=90°,求CP的长;
,b=6,∠C'PC=90°,求CP的长;
(2)连结AC',当以A、B、P、C'为顶点的四边形是平行四边形时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com