
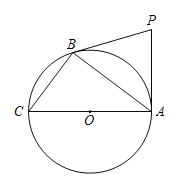
【题目】如图,PA,PB是⊙O的两条切线,A,B是切点,AC是⊙O的直径.
(1)若∠ACB=70°,求∠APB的度数;
(2)连接OP,若AB=8,BC=6,求OP的长.
【答案】(1)∠APB=40°;(2)![]()
【解析】
(1)利用直径所对的圆周角是直角,切线的性质定理证明∠PAB=∠ACB=∠PBA,利用三角形的内角和可得到结论;
(2)连接OP,交AB于点D,证明∠POA=∠ACB,利用等角的三角函数值相等,可得到结论.
解:(1)∵PA,PB是⊙O的两条切线
∴PA⊥OA,PA =PB
![]()
∵ AC为是⊙O的直径
∴∠ABC=90°
∴∠ACB+∠BAC=90°
又∵∠PAB+∠BAC=90°
∴∠PAB=∠ACB=∠PBA=70°
∴∠APB=40°
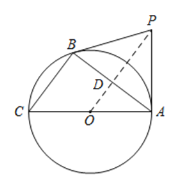
(2)连接OP,交AB于点D
在Rt△ABC中,
∴AC=![]() =10,AO=5
=10,AO=5
∵PA,PB是⊙O的两条切线
∴PO平分∠APB
又∵PA =PB,![]()
∴BD=AD=4,PO⊥AB,
∴PO∥BC
∴∠POA=∠ACB
∴![]() =
=![]() =
=![]() =
=![]()
∴![]() =
=![]() =
=![]() =
=![]()
∴PO =![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
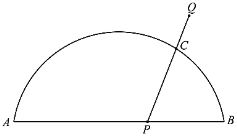
【题目】如图,![]() 是
是![]() 与弦
与弦![]() 所围成图形的外部的一定点,
所围成图形的外部的一定点,![]() 是弦
是弦![]() 上的一动点,连接
上的一动点,连接![]() 交
交![]() 于点
于点![]() .已知
.已知![]() ,设
,设![]() ,
,![]() 两点间的距离为
两点间的距离为![]() ,
,![]() ,
,![]() 两点间的距离为
两点间的距离为![]() ,
,![]() ,
,![]() 两点间的距离为
两点间的距离为![]() .
.
小石根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
(1)按照下表中自变量![]() 的值进行取点、画图、测量分别得到了
的值进行取点、画图、测量分别得到了![]() ,
,![]() 与
与![]() 的几组对应值:
的几组对应值:
| 0 | 1 | 2 | 3 | 4 | 5 | 5.40 | 6 |
| 4.63 | 3.89 | 2.61 | 2.15 | 1.79 | 1.63 | 0.95 | |
| 1.20 | 1.11 | 1.04 | 0.99 | 1.02 | 1.21 | 1.40 | 2.21 |
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() ,
,![]() 的图象;
的图象;
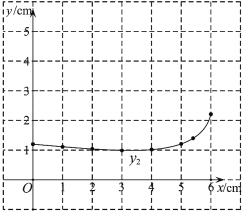
(3)结合函数图象,解决问题:当![]() 为
为![]() 的中点时,
的中点时,![]() 的长度约为______
的长度约为______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:
我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.
求证:BD是四边形ABCD的“相似对角线”;
(3)如图3,已知FH是四边形EFCH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为2![]() ,求FH的长.
,求FH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2012年4月5日下午,重庆一中初2013级“智力快车”比赛的决赛在渝北校区正式进行.“智力快车”活动是我校综合实践课程的传统版块,已有多年历史,比赛试题的内容涉及到文史艺哲科技等多个方面.随着时代的变化,其活动项目也在不断更新.今年的比赛除了继承传统的“快速判断”、“猜猜看”、“英语平台”、“风险提速”四个环节外,特新增了“动手动脑”一项.比赛结束后,一综合实践小组成员就新增环节的满意程度,对现场的观众进行了抽样调查,给予评分,其中:非常满意——5分,满意——4分,一般——3分,有待改进——2分,并将调查结果制作成了如下的两幅不完整的统计图:
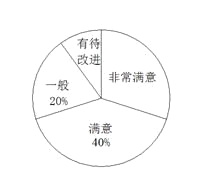
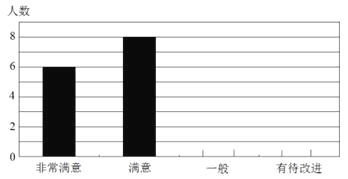

![]()
(1)本次共调查了 名同学,本次调查同学评分的平均得分为 分;
(2)将条形统计图补充完整;
(3)如果评价为“一般”的只有一名是男生,评价为“有待改进”的只有一名是女生,
针对“动手动脑”环节的情况,综合实践小组的成员分别从评价为“一般”和评价
为“有待改进”的两组中,分别随机选出一名同学谈谈意见和建议,请你用列表或画树状图的方法求出所选两名同学刚好都是女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,边长为2的等边△ABC是三棱镜的一个横截面.一束光线ME沿着与AB边垂直的方向射入到BC边上的点D处(点D与B,C不重合),反射光线沿DF的方向射出去,DK与BC垂直,且入射光线和反射光线使∠MDK=∠FDK.设BE的长为x,△DFC的面积为y,则下列图象中能大致表示y与x的函数关系的是( )
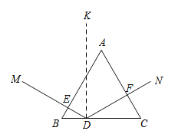
A. B.
B.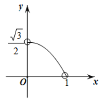 C.
C.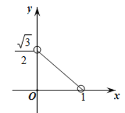 D.
D.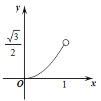
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=30°,AB=AC,将线段AC绕点A逆时针旋转α°(0<α<180),得到线段AD,连接BD,交AC于点P.
(1)当α=90时,
①依题意补全图形;
②求证:PD=2PB;
(2)写出一个α的值,使得PD=![]() PB成立,并证明.
PB成立,并证明.
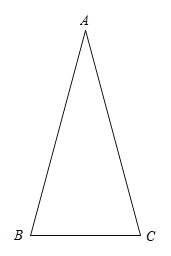
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=6,BC=4,AD是BC边上的高,AM是△ABC外角∠CAE的平分线.以点D为圆心,适当长为半径画弧,交DA于点G,交DC于点H.再分别以点G、H为圆心,大于![]() GH的长为半径画弧,两弧在∠ADC内部交于点Q,连接DQ并延长与AM交于点F,则DF的长度为( ).
GH的长为半径画弧,两弧在∠ADC内部交于点Q,连接DQ并延长与AM交于点F,则DF的长度为( ).
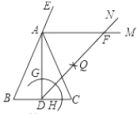
A.6B.![]() C.
C.![]() D.8
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
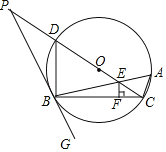
【题目】如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD.
(1)求证:PG与⊙O相切;
(2)若![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,若⊙O的半径为8,PD=OD,求OE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com