
【题目】一家经营打印耗材的门店经销各种打印耗材,其中某一品牌硒鼓的进价为![]() 元/个,售价为
元/个,售价为![]() 元/个(
元/个(![]() ).下面是门店在销售一段时间后销售情况的反馈:
).下面是门店在销售一段时间后销售情况的反馈:
①若每个硒鼓按定价30元的8折出售,可获![]() 的利润;
的利润;
②如果硒鼓按30元/个的价格出售,每月可售出500个,在此基础上,售价每增加5元,月销售量就减少50个.
(1)求![]() 的值,并写出该品牌硒鼓每月的销售量
的值,并写出该品牌硒鼓每月的销售量![]() (个)与售价
(个)与售价![]() (元/个)之间的函数关系式,并注明自变量
(元/个)之间的函数关系式,并注明自变量![]() 的取值范围;
的取值范围;
(2)求该耗材店销售这种硒鼓每月获得的利润![]() (元)与售价
(元)与售价![]() (元/个)之间的函数关系式,并求每月获得的最大利润;
(元/个)之间的函数关系式,并求每月获得的最大利润;
(3)在新冠肺炎流行期间,这种硒鼓的进价降低为![]() 元/个,售价为
元/个,售价为![]() 元/个(
元/个(![]() ).耗材店在2月份仍然按照销售量与售价关系不变的方式销售,并决定将当月销售这种硒鼓获得的利润全部捐赠给火神山医院,支援武汉抗击新冠肺炎.若要使这个月销售这种硒鼓获得的利润
).耗材店在2月份仍然按照销售量与售价关系不变的方式销售,并决定将当月销售这种硒鼓获得的利润全部捐赠给火神山医院,支援武汉抗击新冠肺炎.若要使这个月销售这种硒鼓获得的利润![]() (元)随售价
(元)随售价![]() (元/个)的增大而增大,请直接写出
(元/个)的增大而增大,请直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]() ,当售价为48元/个时,每月获得的利润最大,最大利润为8960元;(3)
,当售价为48元/个时,每月获得的利润最大,最大利润为8960元;(3)![]() .
.
【解析】
(1)由于某一品牌硒鼓的进价为![]() 元/个,根据“按定价30元的8折出售,可获
元/个,根据“按定价30元的8折出售,可获![]() 的利润”可列方程,求出a的值即可;根据“当售价每个为30元时,销售量为500个,若售价每增加5元,月销售量就减少50个”,即可得出y关于x的函数关系式;
的利润”可列方程,求出a的值即可;根据“当售价每个为30元时,销售量为500个,若售价每增加5元,月销售量就减少50个”,即可得出y关于x的函数关系式;
(2)设利润为W,根据“总利润=单个利润×销售量”,即可得出W关于x的函数关系式,代入x=48即可得出结论;
(3)首先求出![]()
![]() ,得其对称轴方程
,得其对称轴方程![]() ,求出n的取值即可.
,求出n的取值即可.
(1)∵硒鼓的进价为![]() 元/个,
元/个,
∴可得,![]() ,解得
,解得![]() .
.
根据题意得,![]() ,即
,即![]() .
.
(2)根据题意,得![]()
![]() .
.
∵![]() ,销售单价不能超过48元/个,
,销售单价不能超过48元/个,
即当![]() 时,
时,![]() 随
随![]() 的增大而增大,
的增大而增大,
∴当![]() 时,
时,![]() 有最大值,最大值为8960.
有最大值,最大值为8960.
答:当售价为48元/个时,每月获得的利润最大,最大利润为8960元.
(3)![]() .
.
根据题意,得
![]()
![]() ,
,
对称轴![]() .
.
∵![]() ,
,
∵当![]() 时,该商品利润
时,该商品利润![]() 随
随![]() 的增大而增大,
的增大而增大,
∴![]() ,解得
,解得![]() .
.
∵进价是降低的,
∴![]() 的取值范围是
的取值范围是![]() .
.


科目:初中数学 来源: 题型:
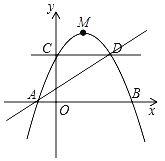
【题目】如图,已知顶点为M(![]() ,
,![]() )的抛物线过点D(3,2),交x轴于A,B两点,交y轴于点C,点P是抛物线上一动点.
)的抛物线过点D(3,2),交x轴于A,B两点,交y轴于点C,点P是抛物线上一动点.
(1)求抛物线的解析式;
(2)当点P在直线AD上方时,求△PAD面积的最大值,并求出此时点P的坐标;
(3)过点P作直线CD的垂线,垂足为Q,若将△CPQ沿CP翻折,点Q的对应点为Q'.是否存在点P,使Q'恰好落在x轴上?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲,乙两个电子团队整理一批电脑数据,整理电脑的台数为![]() (台)与整理需要的时间
(台)与整理需要的时间![]() 之间关系如下图所示,请依据图象提供的信息解答下列问题:
之间关系如下图所示,请依据图象提供的信息解答下列问题:
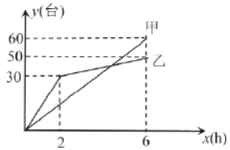
(1)乙队工作![]() 小时整理_____台电脑,工作
小时整理_____台电脑,工作![]() 时两队一共整理了_______台;
时两队一共整理了_______台;
(2)求甲、乙两队![]() 与
与![]() 的关系式.
的关系式.
(3)甲、乙两队整理电脑台数相等时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
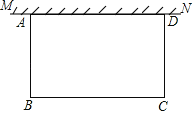
【题目】如图,在足够大的空地上有一段长为a(a≥50)米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在三角形纸板![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上的一个点(不与点
上的一个点(不与点![]() 重合),沿
重合),沿![]() 折叠纸板,点
折叠纸板,点![]() 的对应点是点
的对应点是点![]() .
.
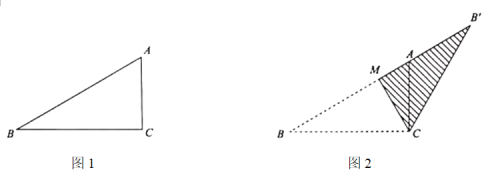
(1)如图2,当点![]() 在射线
在射线![]() 上时,
上时,![]() ________°.
________°.
(2)若![]() ,且点
,且点![]() 不在直线
不在直线![]() 右侧,则点
右侧,则点![]() 到
到![]() 的距离是__________
的距离是__________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.
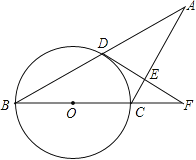
(1)求证:AD=BD;
(2)求证:DF是⊙O的切线
(3)若⊙O直径为18,![]() ,求DE的长
,求DE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A、B在直线MN上(A在B的左侧),点P是直线MN上方一点.若∠PAN=x°,∠PBN=y°,记< x,y >为P的双角坐标.例如,若△PAB是等边三角形,则点P的双角坐标为< 60,120 >.
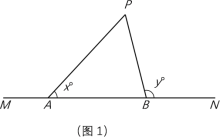

(1)如图2,若AB=22 cm,P<26.6,58>,求△PAB的面积;
(参考数据:tan26.6°≈0.50,tan58°≈1.60.)
(2)在图3中用直尺和圆规作出点P < x,y >,其中y=2x且y=x+30.(保留作图痕迹)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
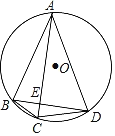
【题目】如图,四边形ABCD内接于⊙O,AC⊥BD于E.
(1)用尺规作图作DF⊥AB于F,交AC于G,并标出F、G(保留作图痕迹,不写作法);
(2)在(1)中,若∠BAD=45°,求证:EG=EC.
查看答案和解析>>
科目:初中数学 来源: 题型:
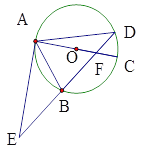
【题目】如图,已知⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB;
(1)求证:AE是⊙O的切线;
(2)已知点B是EF的中点,求证:△EAF∽△CBA
(3)已知AF=4,CF=2,在(2)的条件下,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com