
【题目】如图1,点A、B在直线MN上(A在B的左侧),点P是直线MN上方一点.若∠PAN=x°,∠PBN=y°,记< x,y >为P的双角坐标.例如,若△PAB是等边三角形,则点P的双角坐标为< 60,120 >.
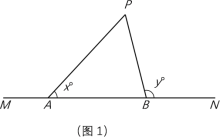

(1)如图2,若AB=22 cm,P<26.6,58>,求△PAB的面积;
(参考数据:tan26.6°≈0.50,tan58°≈1.60.)
(2)在图3中用直尺和圆规作出点P < x,y >,其中y=2x且y=x+30.(保留作图痕迹)
![]()
【答案】(1)S△PAB=176 cm2;(2)见解析.
【解析】
(1)过P作PC⊥AB,垂足为C,则∠PCA=90°,利用三角函数求解即可;
(2)通过y=2x且y=x+30,得到x=30,y=60,可通过作等边三角形的方法作出点P.
(1)解:过P作PC⊥AB,垂足为C,则∠PCA=90°.

在Rt△PBC中,∠PBC=58°,
∵ tan58°=![]() ,
,
∴ BC=![]() ,
,
在Rt△PAC中,∠PAC=26.6°,
∵ tan26.6°=![]() ,
,
∴ AC=![]() ,
,
∵ AB=AC-BC,
∴ ![]() -
-![]() =22.
=22.
解得PC≈16 cm.
∴ S△PAB=![]() ×22×16=176 cm2.
×22×16=176 cm2.
(2)∵y=2x且y=x+30,
∴2x=x+30,
即x=30,y=60,
以B为圆心AB长为半径画弧,再以A为圆心AB长为半径画弧交之前的弧于点O,然后以O为圆心AB长为半径画弧,即可得到点P,
如图,点P即为所求.



科目:初中数学 来源: 题型:
【题目】港口 A、B、C 依次在同一条直线上,甲、乙两艘船同时分别从 A、B两港出发,匀速驶向 C 港,甲、乙两船与 B 港的距离 y(海里)与行驶时间 x 时)之间的函数关系如图所示,则下列说法错误的是( )
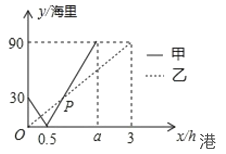
A.甲船平均速度为 60 海里/时B.乙船平均速度为 30 海里/时
C.甲、乙两船在途中相遇两次D.A、C 两港之间的距离为 120 海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 是边
是边![]() 上的一点(不与点
上的一点(不与点![]() 重合),边
重合),边![]() 上点
上点![]() 在点
在点![]() 的右边且
的右边且![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() .
.
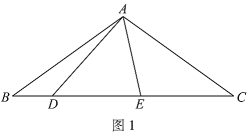
(1)如图1,
①依题意补全图1;
②求证:![]() ;
;
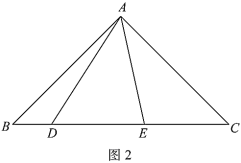
(2)如图2,![]() ,用等式表示线段
,用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家经营打印耗材的门店经销各种打印耗材,其中某一品牌硒鼓的进价为![]() 元/个,售价为
元/个,售价为![]() 元/个(
元/个(![]() ).下面是门店在销售一段时间后销售情况的反馈:
).下面是门店在销售一段时间后销售情况的反馈:
①若每个硒鼓按定价30元的8折出售,可获![]() 的利润;
的利润;
②如果硒鼓按30元/个的价格出售,每月可售出500个,在此基础上,售价每增加5元,月销售量就减少50个.
(1)求![]() 的值,并写出该品牌硒鼓每月的销售量
的值,并写出该品牌硒鼓每月的销售量![]() (个)与售价
(个)与售价![]() (元/个)之间的函数关系式,并注明自变量
(元/个)之间的函数关系式,并注明自变量![]() 的取值范围;
的取值范围;
(2)求该耗材店销售这种硒鼓每月获得的利润![]() (元)与售价
(元)与售价![]() (元/个)之间的函数关系式,并求每月获得的最大利润;
(元/个)之间的函数关系式,并求每月获得的最大利润;
(3)在新冠肺炎流行期间,这种硒鼓的进价降低为![]() 元/个,售价为
元/个,售价为![]() 元/个(
元/个(![]() ).耗材店在2月份仍然按照销售量与售价关系不变的方式销售,并决定将当月销售这种硒鼓获得的利润全部捐赠给火神山医院,支援武汉抗击新冠肺炎.若要使这个月销售这种硒鼓获得的利润
).耗材店在2月份仍然按照销售量与售价关系不变的方式销售,并决定将当月销售这种硒鼓获得的利润全部捐赠给火神山医院,支援武汉抗击新冠肺炎.若要使这个月销售这种硒鼓获得的利润![]() (元)随售价
(元)随售价![]() (元/个)的增大而增大,请直接写出
(元/个)的增大而增大,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=45°,∠ABC=60°,AB=4,D是边BC上的一个动点,以AD为直径画⊙O分别交AB、AC于点E、F,则弦EF长度的最小值为( )

A.![]() B.
B.![]() C.2
C.2![]() D.2
D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (
(![]() 是常数,
是常数,![]() )与
)与![]() 轴交于
轴交于![]() 两点,顶点
两点,顶点![]() 给出下列结论:①
给出下列结论:①![]() ;②若
;②若![]() 在抛物线上,则
在抛物线上,则![]() ;③关于
;③关于![]() 的方程
的方程![]() 有实数解,则
有实数解,则![]() ;④当
;④当![]() 时,
时,![]() 为等腰直角三角形,其中正确的结论是( )
为等腰直角三角形,其中正确的结论是( )
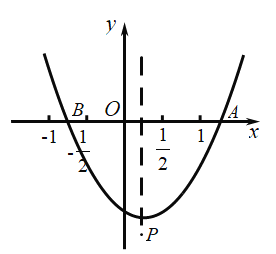
A.①②B.①③C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1.
(1)求抛物线L的解析式;
(2)将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围;
(3)设点P是抛物线L上任一点,点Q在直线l:x=﹣3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2008年5月1日,目前世界上最长的跨海大桥——杭州湾跨海大桥通车了.通车后,苏南A地到宁波港的路程比原来缩短了120千米.已知运输车速度不变时,行驶时间将从原来的3时20分缩短到2时.
(1)求跨海大桥到宁波港的路程.
(2)若货物运输费用=A地经杭州湾包括运输成本和时间成本,已知某车货物从A地到宁波港的运输成本是每千米1.8元,时间成本是每时28元,那么该车货物从A地经杭州湾跨海大桥到宁波港的运输费用是多少元?
(3)A地准备开辟宁波方向的外运路线,即货物从A地经杭州湾跨海大桥到宁波港,再从宁波港运到B地.若有一批货物(不超过10车)从A地按外运路线运到B地的运费需8320元,其中从A地经杭州湾跨海大桥到宁波港的每车运输费用与(2)中相同,从宁波港到B地的海上运费对一批不超过10车的货物计费方式是:一车800元,当货物每增加1车时,每车的海上运费就减少20元,问这批货物有几车?
查看答案和解析>>
科目:初中数学 来源: 题型:
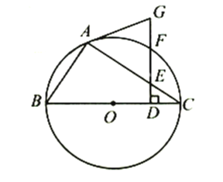
【题目】如图,![]() 为⊙
为⊙![]() 的内接三角形,
的内接三角形,![]() 为⊙
为⊙![]() 的直径,在线段
的直径,在线段![]() 上取点
上取点![]() (不与端点重合),作
(不与端点重合),作![]() ,分别交
,分别交![]() 、圆周于
、圆周于![]() 、
、![]() ,连接
,连接![]() ,已知
,已知![]() .
.
(1)求证:![]() 为⊙
为⊙![]() 的切线;
的切线;
(2)已知![]() ,填空:
,填空:
①当![]() __________
__________![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②若![]() ,当
,当![]() __________时,
__________时,![]() 为等腰直角三角形.
为等腰直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com