
【题目】如图,△ABC中,∠BAC=45°,∠ABC=60°,AB=4,D是边BC上的一个动点,以AD为直径画⊙O分别交AB、AC于点E、F,则弦EF长度的最小值为( )

A.![]() B.
B.![]() C.2
C.2![]() D.2
D.2![]()
【答案】B
【解析】
作AH⊥BC于H,OG⊥EF于G,连接OE、OF,如图,利用圆周角定理得∠EOF=120°,利用含30度的直角三角形三边的关系得到EF=2EG=![]() OE,所以当⊙O的半径最小时,EF的值最小,此时AD最小,AD的最小值为AH的长,然后计算出AH的长就可得到EF的最小值.
OE,所以当⊙O的半径最小时,EF的值最小,此时AD最小,AD的最小值为AH的长,然后计算出AH的长就可得到EF的最小值.
作AH⊥BC于H,OG⊥EF于G,连接OE、OF,如图,
∵∠EOF=2∠EAF=2×60°=120°,OE=OF,
∴∠OEF=30°,
∴OG=![]() OE,
OE,
∴EG=![]() OG,
OG,
∵OG⊥EF,
∴EG=FG=![]() OE,
OE,
∴EF=2EG=![]() OE,
OE,
当OE的值最小时,EF的值最小,
此时AD最小,AD的最小值为AH的长,
在Rt△ABH中,∵∠ABH=45°,
∴AH=![]() AB=2
AB=2![]() ,
,
∴OE的最小值为![]() ,
,
∴EF的最小值为![]() ×
×![]() =
=![]() .
.
故选:B.



科目:初中数学 来源: 题型:
【题目】如图是某地下停车库入口的设计示意图,已知AB⊥BD,坡道AD的坡度i=1:2.4(指坡面的铅直高度BD与水平宽度AB的比),AB=7.2 m,点C在BD上,BC=0.4 m,CE⊥AD.按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,请根据以上数据,求出该地下停车库限高CE的长.
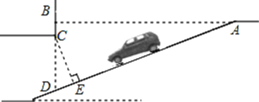
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗击新冠肺炎疫情期间,老百姓越来越依赖电商渠道获取必要的生活资料.小石经营的水果店也适时加入了某电商平台,并对销售的水果中的部分(如下表)进行促销:参与促销的水果免配送费且一次购买水果的总价满128元减![]() 元.每笔订单顾客网上支付成功后,小石会得到支付款的80%.
元.每笔订单顾客网上支付成功后,小石会得到支付款的80%.
参与促销水果 | |
水果 | 促销前单价 |
苹果 | 58元/箱 |
耙耙柑 | 70元/箱 |
车厘子 | 100元/箱 |
火龙果 | 48元/箱 |
(1)当![]() 时,某顾客一次购买苹果和车厘子各1箱,需要支付_____元,小石会得到______元;
时,某顾客一次购买苹果和车厘子各1箱,需要支付_____元,小石会得到______元;
(2)在促销活动中,为保障小石每笔订单所得到的金额不低于促销前总价的七折,则![]() 的最大值为_____.
的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在三角形纸板![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上的一个点(不与点
上的一个点(不与点![]() 重合),沿
重合),沿![]() 折叠纸板,点
折叠纸板,点![]() 的对应点是点
的对应点是点![]() .
.
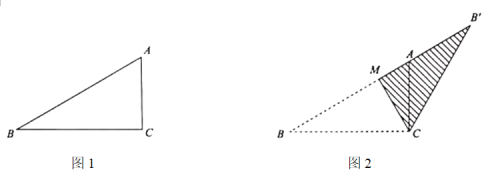
(1)如图2,当点![]() 在射线
在射线![]() 上时,
上时,![]() ________°.
________°.
(2)若![]() ,且点
,且点![]() 不在直线
不在直线![]() 右侧,则点
右侧,则点![]() 到
到![]() 的距离是__________
的距离是__________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某县2015年初中毕业生数学质量检测成绩等级的分布情况,随机抽取了该县若干名初中毕业生的数学质量检测成绩,按A,B,C,D四个等级进行统计分析,并绘制了如下尚不完整的统计图:

请根据以上统计图提供的信息,解答下列问题:
(1)本次抽取的学生有 名;补全条形统计图1;
(2)根据调查结果,请估计该县1430名初中毕业生数学质量检测成绩为A级的人数是
(3)某校A等级中有甲、乙、丙、丁4名学生成绩并列第一,现在要从这4位学生中抽取2名学生在校进行学习经验介绍,用列举法求出恰好选中甲乙两位学生的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A、B在直线MN上(A在B的左侧),点P是直线MN上方一点.若∠PAN=x°,∠PBN=y°,记< x,y >为P的双角坐标.例如,若△PAB是等边三角形,则点P的双角坐标为< 60,120 >.
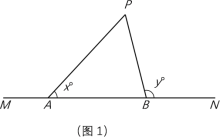

(1)如图2,若AB=22 cm,P<26.6,58>,求△PAB的面积;
(参考数据:tan26.6°≈0.50,tan58°≈1.60.)
(2)在图3中用直尺和圆规作出点P < x,y >,其中y=2x且y=x+30.(保留作图痕迹)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图.

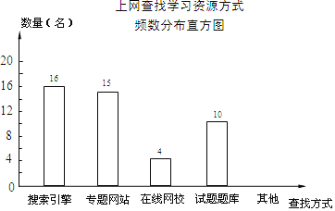
(1)频数分布表中![]() 的值:
的值:![]() _____________,
_____________,![]() ______________;
______________;
(2)补全频数分布直方图;
(3)若全校有1000名学生,估计该校利用搜索引擎上网查找学习资源的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骑行是现在流行的健身方式之一,周末“绿色骑行俱乐部”组织了一次从甲地出发,目的地为乙地的骑行活动,在“俱乐部”自行车队出发1小时后,恰有一辆摩托车从甲地出发,沿自行车队行进路线前往乙地,到达乙地后立即按原路返回甲地.自行车队与摩托车行驶速度均保持不变,并且摩托车行驶速度是自行车队行驶速度的3倍.如图所示的是自行车队、摩托车离甲地的路程![]() 与自行车队离开甲地的时间
与自行车队离开甲地的时间![]() 的关系图象,请根据图象提供的信息,回答下列问题.
的关系图象,请根据图象提供的信息,回答下列问题.
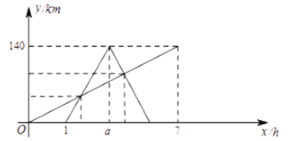
(1)摩托车行驶的速度是__________;![]() ____________;
____________;
(2)求出自行车队离甲地的路程![]() 与自行车队离开甲地的时间
与自行车队离开甲地的时间![]() 的关系式,并求出自行车队出发多少小时与摩托车相遇;
的关系式,并求出自行车队出发多少小时与摩托车相遇;
(3)直接写出当摩托车与自行车队相距![]() 时,此时离摩托车出发经过了多少小时.
时,此时离摩托车出发经过了多少小时.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com