练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一组数据－2、0、－3、－2、－3、1、x的众数是－3，则这组数据的中位数是 ．

    【答案】

    【解析】

    找中位数要把数据按从小到大的顺序排列，位于最中间的一个数（或两个数的平均数）为中位数；众数是一组数据中出现次数最多的数据，注意众数可以不只一个．

    解：∵-2、0、-3、-2、-3、1、x的众数是-3，

    ∴x=-3，

    先对这组数据按从小到大的顺序重新排序-3、-3、-3、-2、-2、0、1位于最中间的数是-2，

    ∴这组数的中位数是-2．

    故答案为-2．

    本题属于基础题，考查了确定一组数据的中位数和众数的能力．一些学生往往对这个概念掌握不清楚，计算方法不明确而误选其它选项，注意找中位数的时候一定要先排好顺序，然后再根据奇数和偶数个来确定中位数，如果数据有奇数个，则正中间的数字即为所求，如果是偶数个则找中间两位数的平均数

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某地为了促进旅游业的发展，要在如图所示的三条公路，，围成的一块地上修建一个度假村，要使这个度假村到，两条公路的距离相等，且到，两地的距离相等，下列选址方法绘图描述正确的是（ ）

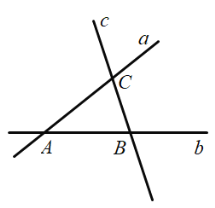
    A.画的平分线，再画线段的垂直平分线，两线的交点符合选址条件

    B.先画和的平分线，再画线段的垂直平分线，三线的交点符合选址条件

    C.画三个角，和三个角的平分线，交点即为所求

    D.画，，三条线段的垂直平分线，交点即为所求

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠BAC＝45°，∠ABC＝60°，AB＝4，D是边BC上的一个动点，以AD为直径画⊙O分别交AB、AC于点E、F，则弦EF长度的最小值为（ ）

    A.B.C.2D.2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线L：y=ax2+bx+c与x轴交于A、B（3，0）两点（A在B的左侧），与y轴交于点C（0，3），已知对称轴x=1．

    （1）求抛物线L的解析式；

    （2）将抛物线L向下平移h个单位长度，使平移后所得抛物线的顶点落在△OBC内（包括△OBC的边界），求h的取值范围；

    （3）设点P是抛物线L上任一点，点Q在直线l：x=﹣3上，△PBQ能否成为以点P为直角顶点的等腰直角三角形？若能，求出符合条件的点P的坐标；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某水果店计划购进甲、乙两种高档水果共400千克，每千克的售价、成本与购进数量（千克）之间关系如表：

    每千克售价（元）

    每千克成本（元）

    甲

    ﹣0.1x+100

    50

    乙

    ﹣0.2x+120（0＜x≤200）

    60

    （200＜x≤400）

    （1）若甲、乙两种水果全部售完，求水果店获得总利润y（元）与购进乙种水果x（千克）之间的函数关系式（其他成本不计）；

    （2）若购进两种水果都不少于100千克，当两种水果全部售完，水果能获得的最大利润．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2008年5月1日，目前世界上最长的跨海大桥——杭州湾跨海大桥通车了．通车后，苏南A地到宁波港的路程比原来缩短了120千米．已知运输车速度不变时，行驶时间将从原来的3时20分缩短到2时．

    （1）求跨海大桥到宁波港的路程．

    （2）若货物运输费用=A地经杭州湾包括运输成本和时间成本，已知某车货物从A地到宁波港的运输成本是每千米1.8元，时间成本是每时28元，那么该车货物从A地经杭州湾跨海大桥到宁波港的运输费用是多少元？

    （3）A地准备开辟宁波方向的外运路线，即货物从A地经杭州湾跨海大桥到宁波港，再从宁波港运到B地．若有一批货物（不超过10车）从A地按外运路线运到B地的运费需8320元，其中从A地经杭州湾跨海大桥到宁波港的每车运输费用与（2）中相同，从宁波港到B地的海上运费对一批不超过10车的货物计费方式是：一车800元，当货物每增加1车时，每车的海上运费就减少20元，问这批货物有几车？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

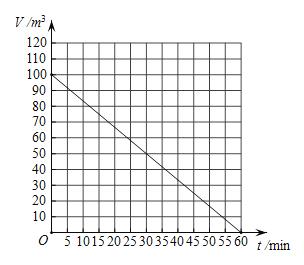
    【题目】如图，是用图象反映储油罐内的油量V与输油管开启时间t的函数关系．观察这个图象，以下结论正确的有________________．

    ①随着输油管开启时间的增加，储油罐内的油量在减少；

    ②输油管开启10分钟时，储油罐内的油量是80立方米；

    ③如果储油罐内至少存油40立方米，那么输油管最多可以开启36分钟；

    ④输油管开启30分钟后，储油罐内的油量只有原油量的一半．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知矩形纸片ABCD，怎样折叠，能使边AB被三等分？

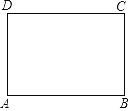
    以下是小红的研究过程．

    思考过程

    要使边AB被三等分，若从边DC上考虑，就是要折出DM＝DC，

    也就是要折出DM＝AB，

    当DB、AM相交于F时，即要折出对角线上的DF＝DB．那么…

    折叠方法和示意图

    ①折出DB；对折纸片，使D、B重合，得到的折痕与DB相交于点E；继续折叠纸片，使D、B与E重合，得到的折痕与DB分别相交于点F、G；

    ②折出AF、CG，分别交边CD、AB于M、Q；

    ③过M折纸片，使D落在MC上，得到折痕MN，则边AB被N、Q三等分．

    （1）整理小红的研究过程，说明AN＝NQ＝QB；

    （2）用一种与小红不同的方法折叠，使边AB被三等分．（需简述折叠方法并画出示意图）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某县教育局为了丰富初中学生的大课间活动，要求各学校开展形式多样的阳光体育活动．某中学就“学生体育活动兴趣爱好”的问题，随机调查了本校某班的学生，并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图：

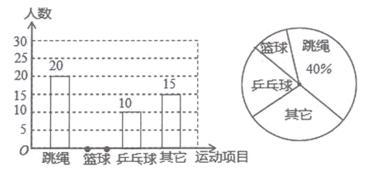
    （1）在这次调查中，共调查了 人，在扇形统计图中，“乒乓球”的百分比为 %，如果学校有800名学生，估计全校学生中有 人喜欢篮球项目；

    （2）请将条形统计图补充完整；

    （3）学校在喜欢篮球的初一学生中挑选了3名同学，分别是李明、林海和陈阳，然后在这3名学生中最终挑选2人参加学校的篮球队，请用列表法或画树状图的方法求出李明最终被选上的概率．

    查看答案和解析>>

    同步练习册答案