
【题目】某水果店计划购进甲、乙两种高档水果共400千克,每千克的售价、成本与购进数量(千克)之间关系如表:
每千克售价(元) | 每千克成本(元) | |
甲 | ﹣0.1x+100 | 50 |
乙 | ﹣0.2x+120(0<x≤200) | 60 |
|
(1)若甲、乙两种水果全部售完,求水果店获得总利润y(元)与购进乙种水果x(千克)之间的函数关系式(其他成本不计);
(2)若购进两种水果都不少于100千克,当两种水果全部售完,水果能获得的最大利润.
【答案】(1)1)当0<x<200时,y=﹣0.3x2+90x+4000,当200≤x≤400时,y=﹣0.1x2+20x+10000;(2)当购进甲种水果150千克、乙种水果250千克时,才能使获得的利润最大,最大利润为10750元.
【解析】
(1)分0<x<200和200≤x≤400两种情况,根据总利润=甲种水果的利润+乙种水果的利润,列出函数解析式;
(2)分100≤x<200和200≤x≤300两种情况,将对应解析式配方成顶点,再利用二次函数的性质求解可得.
解:(1)当0<x<200时,
![]()
![]()
当200≤x≤400时,
![]()
=![]()
(2)由题意得:
![]()
![]()
若100≤x<200,则y=﹣0.3x2+90x+4000=﹣0.3(x﹣150)2+10750,
当x=150时,y的最大值为10750;
若200≤x≤300时,![]()
∵x>100时,y随x的增大而减小,
∴当x=200时,y取得最大值,最大值为10000元;
∵10750>10000,故x=150,
综上,当购进甲种水果150千克、乙种水果250千克时,才能使获得的利润最大.最大利润为10750元.


科目:初中数学 来源: 题型:
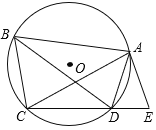
【题目】如图,四边形ABCD内接于⊙O,已知AB=AC,延长CD至点E,使CE=BD,连结AE.
(1)求证:AD平分∠BDE;
(2)若AB∥CD,求证:AE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某县2015年初中毕业生数学质量检测成绩等级的分布情况,随机抽取了该县若干名初中毕业生的数学质量检测成绩,按A,B,C,D四个等级进行统计分析,并绘制了如下尚不完整的统计图:

请根据以上统计图提供的信息,解答下列问题:
(1)本次抽取的学生有 名;补全条形统计图1;
(2)根据调查结果,请估计该县1430名初中毕业生数学质量检测成绩为A级的人数是
(3)某校A等级中有甲、乙、丙、丁4名学生成绩并列第一,现在要从这4位学生中抽取2名学生在校进行学习经验介绍,用列举法求出恰好选中甲乙两位学生的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图.

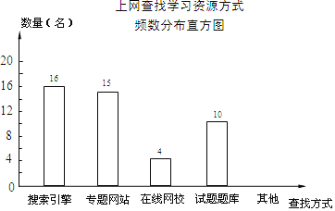
(1)频数分布表中![]() 的值:
的值:![]() _____________,
_____________,![]() ______________;
______________;
(2)补全频数分布直方图;
(3)若全校有1000名学生,估计该校利用搜索引擎上网查找学习资源的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察下列图形与等式的关系,并填空:
第一个图形: ;
;
第二个图形: ;
;
第一个等式:9+4=13;第二个等式:13+8=21;
第三个图形: ;……;
;……;
第三个等式: + = ;……;
(2)根据以上图形与等式的关系,请你猜出第n个等式(用含有n的代数式表示),并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是3,点P是直线BC上一点,连接PA,将线段PA绕点P逆时针旋转90°得到线段PE,在直线BA上取点F,使BF=BP,且点F与点E在BC同侧,连接EF,CF.

(1)如图①,当点P在CB延长线上时,求证:四边形PCFE是平行四边形;
(2)如图②,当点P在线段BC上时,四边形PCFE是否还是平行四边形,说明理由;
(3)在(2)的条件下,四边形PCFE的面积是否有最大值?若有,请求出面积的最大值及此时BP长;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
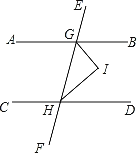
【题目】如图,已知AB∥CD,直线EF分别交直线AB、CD于点G、H,GI、HI分别平分∠BGH、∠GHD.
(1)求证GI⊥HI.
(2)请用文字概括(1)所证明的命题: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() ,
,![]() ,与坐标轴交于A、B两点.
,与坐标轴交于A、B两点.
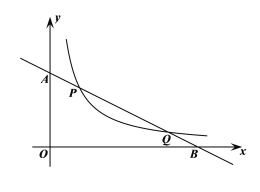
(1)求一次函数与反比例函数的解析式;
(2)观察图象,当![]() 时,直接写出不等式
时,直接写出不等式![]() 的解集;
的解集;
(3)将直线![]() 向下平移
向下平移![]() 个单位,若直线与反比例函数
个单位,若直线与反比例函数![]() 的图象有唯一交点,求
的图象有唯一交点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com