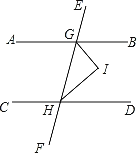
【题目】如图，已知AB∥CD，直线EF分别交直线AB、CD于点G、H，GI、HI分别平分∠BGH、∠GHD．
（1）求证GI⊥HI．
（2）请用文字概括（1）所证明的命题： ．
科目：初中数学 来源： 题型：
【题目】（1）某学校“智慧方园”数学社团遇到这样一个题目：
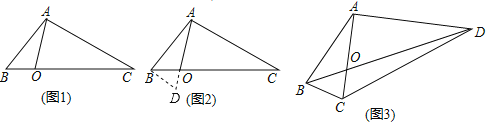
如图1，在△ABC中，点O在线段BC上，∠BAO=30°，∠OAC=75°，AO=
，BO：CO=1：3，求AB的长．
经过社团成员讨论发现，过点B作BD∥AC，交AO的延长线于点D，通过构造△ABD就可以解决问题（如图2）．
请回答：∠ADB= °，AB= ．
（2）请参考以上解决思路，解决问题：
如图3，在四边形ABCD中，对角线AC与BD相交于点O，AC⊥AD，AO=，∠ABC=∠ACB=75°，BO：OD=1：3，求DC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某水果店计划购进甲、乙两种高档水果共400千克，每千克的售价、成本与购进数量（千克）之间关系如表：
每千克售价（元） | 每千克成本（元） | |
甲 | ﹣0.1x+100 | 50 |
乙 | ﹣0.2x+120（0＜x≤200） | 60 |
|
（1）若甲、乙两种水果全部售完，求水果店获得总利润y（元）与购进乙种水果x（千克）之间的函数关系式（其他成本不计）；
（2）若购进两种水果都不少于100千克，当两种水果全部售完，水果能获得的最大利润．
查看答案和解析>>
科目：初中数学 来源： 题型：
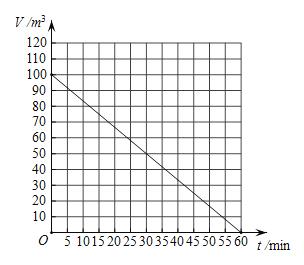
【题目】如图，是用图象反映储油罐内的油量V与输油管开启时间t的函数关系．观察这个图象，以下结论正确的有________________．
①随着输油管开启时间的增加，储油罐内的油量在减少；
②输油管开启10分钟时，储油罐内的油量是80立方米；
③如果储油罐内至少存油40立方米，那么输油管最多可以开启36分钟；
④输油管开启30分钟后，储油罐内的油量只有原油量的一半．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系
中，抛物线
与x轴交于点A和点B（点A在点B左侧），
（1）若抛物线的对称轴是直线x=1，求出点A和点B的坐标，并画出此时函数的图象；
（2）当已知点P（m，2），Q(－m，2m－1)．若抛物线与线段PQ恰有一个公共点，结合函数图象，求m的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知矩形纸片ABCD，怎样折叠，能使边AB被三等分？
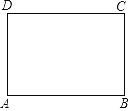
以下是小红的研究过程．
思考过程 | 要使边AB被三等分，若从边DC上考虑，就是要折出DM＝ 也就是要折出DM＝ 当DB、AM相交于F时，即要折出对角线上的DF＝ |
折叠方法和示意图 | ①折出DB；对折纸片，使D、B重合，得到的折痕与DB相交于点E；继续折叠纸片，使D、B与E重合，得到的折痕与DB分别相交于点F、G； ②折出AF、CG，分别交边CD、AB于M、Q； ③过M折纸片，使D落在MC上，得到折痕MN，则边AB被N、Q三等分．
|
（1）整理小红的研究过程，说明AN＝NQ＝QB；
（2）用一种与小红不同的方法折叠，使边AB被三等分．（需简述折叠方法并画出示意图）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中有一个3×3的正方形网格，其右下角格点（小正方形的顶点）A的坐标为（﹣1，1），左上角格点B的坐标为（﹣4，4），若分布在过定点（﹣1，0）的直线y＝﹣k（x+1）两侧的格点数相同，则k的取值可以是（ ）
A.
B.
C.2D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数
的函数图象如图，点
位于坐标原点，点
在
轴的正半轴上，点
在二次函数位于第一象限的图象上，
，
，
，
…都是直角顶点在抛物线上的等腰直角三角形，则
的斜边长为( )
A.20B.
C.22D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC内接于⊙O，∠CBG=∠A，CD为直径，OC与AB相交于点E，过点E作EF⊥BC，垂足为F，延长CD交GB的延长线于点P，连接BD．
（1）求证：PG与⊙O相切；
（2）若
=
，求
的值；
（3）在（2）的条件下，若⊙O的半径为8，PD=OD，求OE的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
