
【题目】如图,已知一次函数![]() 的图象交
的图象交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在射线
在射线![]() 上,且
上,且![]() .
.![]() 垂直
垂直![]() 轴于点
轴于点![]() .
.
![]() 点
点![]() 坐标为________,点
坐标为________,点![]() 坐标为________.
坐标为________.
![]() 操作:将一足够大的三角板的直角顶点
操作:将一足够大的三角板的直角顶点![]() 放在射线
放在射线![]() 或射线
或射线![]() 上,一直角边始终过点
上,一直角边始终过点![]() ,另一直角边与
,另一直角边与![]() 轴相交于点
轴相交于点![]() .问是否存在这样的点
.问是否存在这样的点![]() ,使以点
,使以点![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 全等?若存在,求出点
全等?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1)![]() (2)存在这样的点
(2)存在这样的点![]() ,使以点
,使以点![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 全等
全等
【解析】
(1)根据点E在x轴正半轴上,OE=OF=10,即可得出E(10,0),再根据点F在射线BA上,可设F(x,x+2),则OH=x,FH=x+2,最后根据勾股定理求得x即可;
(2)当点Q在射线HF上时,分两种情况:①QE=OE=10,②QP=OE=10;当点Q在射线AF上时,分两种情况:①QE=OE=10,②QP=OE=10,分别作辅助线构造直角三角形或相似三角形,求得QH的长,即可得出点Q的坐标.
(1)∵点E在x轴正半轴上,OE=OF=10,∴E(10,0).
∵点F在射线BA上,∴可设F(x,x+2),则OH=x,FH=x+2,如图,连接OF,则
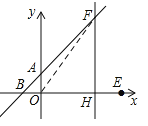
Rt△OHF中,x2+(x+2)2=102,解得:x=6,∴x+2=8,∴F(6,8).
故答案为:(10,0),(6,8);
(2)存在这样的点Q,使以点P,Q,E为顶点的三角形与△POE全等.
当点Q在射线HF上时,分两种情况:
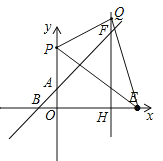
①如图所示,若QE=OE=10,而HE=10﹣6=4,∴在Rt△QHE中,QH=![]() =
=![]() =2
=2![]() ,∴Q(6,2
,∴Q(6,2![]() );
);
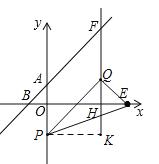
②如图所示,若QP=OE=10,作PK⊥FH于K,则∠PKQ=∠QHE=90°,QK=![]() =8.
=8.
∵∠PQK+∠EQH=∠QEH+∠EQH=90°,∴∠PQK=∠QEH,∴△PQK∽△QEH,∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得:QH=3,∴Q(6,3);
,解得:QH=3,∴Q(6,3);
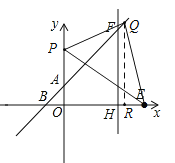
当点Q在射线AF上时,分两种情况:
①如图所示,若QE=OE=10,设Q(x,x+2),作QR⊥x轴于R,则RE=10﹣x,QR=x+2,∴Rt△QRE中,(10﹣x)2+(x+2)2=102,解得:x=4±![]() ,∴Q(4+
,∴Q(4+![]() ,6+
,6+![]() )或(4﹣
)或(4﹣![]() ,6﹣
,6﹣![]() );
);
②如图所示,若QP=OE=10,则QE=OP,设Q(x,x+2).
∵∠POE=90°,∴四边形OPQE是矩形,∴x=OE=10.
∵Q在射线AF上,∴x+2=QE=12,∴Q(10,12).


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
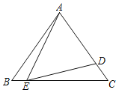
【题目】如图,在△ABC中,AB=AC=6,点D在边AC上,AD的中垂线交BC于点E.若∠AED=∠B,CE=3BE,则CD等于( )
A. ![]() B. 2C.
B. 2C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在他家里的时钟上安装了一个电脑软件,他设定当钟声在n点钟响起后,下一次则在(3n﹣1)小时后响起,例如钟声第一次在3点钟响起,那么第2次在(3×3﹣1=8)小时后,也就是11点响起,第3次在(3×11﹣1=32)小时后,即7点响起,以此类推…;现在第1次钟声响起时为2点钟,那么第3次响起时为_____点,第2017次响起时为_____点(如图钟表,时间为12小时制).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠B=30°,O是BC上一点,以点O为圆心,OB长为半径作圆,恰好经过点A,并与BC交于点D.
(1)判断直线CA与⊙O的位置关系,并说明理由;
(2)若AB=4![]() ,求图中阴影部分的面积(结果保留π).
,求图中阴影部分的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是2018年12月份的日历,我们选择其中的方框部分,将每个方框部分中4个位置上的数交叉求平方和,再相减,例如:(32+112)-(42+102)=14,(212+292)-(222+282)=14,不难发现结果都是14.
(1)今天是12月12日,请你写一个含今天日期在内的类似部分的算式;
(2)请你利用整式的运算对以上规律加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,在由边长为1的正方形组成的网络纸中有四边形![]() .
.
①利用网格作出边![]() 的垂直平分线
的垂直平分线![]() 、
、![]() 的垂直平分线
的垂直平分线![]() ;
;
②设①中![]() 、
、![]() 两条直线交于点
两条直线交于点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,判断:
,判断:![]() _____
_____![]() ,
,![]() _____
_____![]() (用“
(用“![]() ”、“
”、“![]() ”或“
”或“![]() ”填空);
”填空);
③在直线![]() 上取点
上取点![]() ,使得
,使得![]() 值最小.
值最小.
(2)在由边长为1的正方形组成的网格纸中,已知线段![]() 、
、![]() ,请在网格纸中分别画出两个不同的
,请在网格纸中分别画出两个不同的![]() ,使得
,使得![]() ,高
,高![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若经过一个三角形某一顶点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形为等腰三角形过该顶点的生成三角形.

(1)如图,在等腰Rt△ABC中,AB=AC,∠A=90°,请问△ABC是否是生成三角形?请你说明理由.
(2)若△ABC是等腰三角形过顶点B的生成三角形,∠C是其最小的内角,请探求∠ABC与∠C之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:①1=12;②2+3+4=32;③3+4+5+6+7=52;④4+5+6+7+8+9+10=72;…请根据上述规律判断下列等式正确的是( )
A. 1008+1009+…+3025=20162 B. 1009+1010+…+3026=20172
C. 1009+1010+…+3025=20172 D. 1010+1011+…+3029=20192
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com