
【题目】综合与探究
如图所示:点![]() 和点
和点![]() 分别在射线
分别在射线![]() 和射线
和射线![]() 上运动(点
上运动(点![]() 和点
和点![]() 不与点
不与点![]() 重合),
重合),![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 在顶点
在顶点![]() 处的外角平分线,
处的外角平分线,![]() 的反向延长线与
的反向延长线与![]() 交于点
交于点![]() .试回答下列问题:
.试回答下列问题:
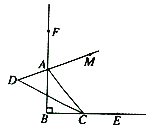
(1)若![]() ,则
,则![]() _________
_________![]() ,若
,若![]() ,则
,则![]() _________
_________![]() .
.
(2)设![]() ,用
,用![]() 表示
表示![]() 的度数,则
的度数,则![]() __________
__________![]() .
.
(3)试猜想,点![]() 和点
和点![]() 在运动过程中,
在运动过程中,![]() 的度数是否发生变化?若变化,请求出变化范围;若不变,请给出证明.
的度数是否发生变化?若变化,请求出变化范围;若不变,请给出证明.
【答案】(1)45 45;(2)![]() ;(3)不变,理由如下:
;(3)不变,理由如下:
【解析】
(1)根据角平分线的定义用∠ACB表示出∠ACD,再根据三角形的一个外角等于与它不相邻的两个内角的和与角平分线的定义表示出∠MAC,整理即可得解;
(2)根据(1)可得∠D=45°,然后根据三角形的一个外角等于与它不相邻的两个内角的和解答即可;
(3)根据角的平分线定义表示出∠MAC,∠ACD,再根据三角形的一个外角等于与它不相邻的两个内角的和列式整理即可得到∠D的大小只与∠ABC有关.
(1)∵CD是∠ACB的平分线,
∴∠ACD=![]() ∠ACB,
∠ACB,
∵AM是△ABC在顶点A处的外角平分线,
∴∠MAC=![]() ∠FAC,
∠FAC,
根据三角形外角性质,∠MAC=∠ACD+∠D,
∠FAC=∠ACB+∠ABC,
∴∠ACD+∠D=![]() (∠ACB+∠ABC),
(∠ACB+∠ABC),
∴![]() ∠ACB+∠D=
∠ACB+∠D=![]() ∠ACB+
∠ACB+![]() ∠ABC,
∠ABC,
∠D=![]() ∠ABC,
∠ABC,
∵BF⊥BE,
∴∠ABC=90°,
∴∠D=![]()
即∠D的大小与∠ACB无关,等于![]() ∠ABC,
∠ABC,
当∠ACB=30°,∠D=45°,∠ACB=70°,∠D=45°;
(2)根据(1)∠D=45°,
∵∠ACD=x,
∴在△ACD中,∠MAC=∠ACD+∠D=(45+x)°;
(3)不变.理由如下:
∵CD是∠ACB的平分线,
∴∠ACD=![]() ∠ACB,
∠ACB,
∵AM是△ABC在顶点A处的外角平分线,
∴∠MAC=![]() ∠FAC,
∠FAC,
根据三角形外角性质,∠MAC=∠ACD+∠D,
∠FAC=∠ACB+∠ABC,
∴∠ACD+∠D=![]() (∠ACB+∠ABC),
(∠ACB+∠ABC),
∴![]() ∠ACB+∠D=
∠ACB+∠D=![]() ∠ACB+
∠ACB+![]() ∠ABC,
∠ABC,
∠D=![]() ∠ABC,
∠ABC,
∵BF⊥BE,
∴∠ABC=90°,
∴∠D=![]() ×90°=45°.
×90°=45°.


科目:初中数学 来源: 题型:
【题目】某农场去年种植了10亩地的南瓜,亩产量为2000kg,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,设南瓜种植面积的增长率为x.
(1)则今年南瓜的种植面积为 亩;(用含x的代数式表示)
(2)如果今年南瓜亩产量的增长率是种植面积的增长率的![]() ,今年南瓜的总产量为60000kg,求南瓜亩产量的增长率.
,今年南瓜的总产量为60000kg,求南瓜亩产量的增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教室里有4排日光灯,每排灯各由一个开关控制,但灯的排数序号与开关序号不一定对应,其中控制第二排灯的开关已坏(闭合开关时灯也不亮).
(1)将4个开关都闭合时,教室里所有灯都亮起的概率是 ;
(2)在4个开关都闭合的情况下,不知情的雷老师准备做光学实验,由于灯光太强,他需要关掉部分灯,于是随机将4个开关中的2个断开,请用列表或画树状图的方法,求恰好关掉第一排与第三排灯的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是过
是过![]() 点的一条直线,且
点的一条直线,且![]() 、
、![]() 在
在![]() 的异侧,
的异侧,![]() 于
于![]() ,
,![]() 于
于![]() .
.
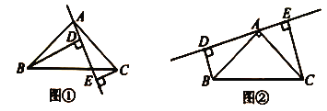
(1)求证:![]() .
.
(2)若将直线![]() 绕点
绕点![]() 旋转到图②的位置时(
旋转到图②的位置时(![]() ),其余条件不变,问
),其余条件不变,问![]() 与
与![]() 、
、![]() 的关系如何?请予以证明.
的关系如何?请予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(组)解应用题:
为顺利通过国家义务教育均衡发展验收,我市某中学配备了两个多媒体教室,购买了笔记本电脑和台式电脑共120台,购买笔记本电脑用了7.2万元,购买台式电脑用了24万元,已知笔记本电脑单价是台式电脑单价的1.5倍,那么笔记本电脑和台式电脑的单价各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
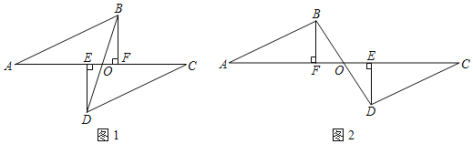
【题目】已知点A、E、F、C在一条直线上,AE=CF,过点E、F分别作DE⊥AC,BF⊥AC,且AB=CD.连接BD,交AC于点O.
(1)如图1,求证:BF=DE.
(2)将△DEC沿AC方向平移到如图2的位置,其余条件不变,若BF=3cm,请直接写出DE的长是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com