
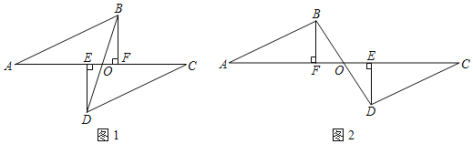
【题目】已知点A、E、F、C在一条直线上,AE=CF,过点E、F分别作DE⊥AC,BF⊥AC,且AB=CD.连接BD,交AC于点O.
(1)如图1,求证:BF=DE.
(2)将△DEC沿AC方向平移到如图2的位置,其余条件不变,若BF=3cm,请直接写出DE的长是多少?
【答案】(1)证明见解析;(2)DE=3cm.
【解析】
(1)首先由题意推出AF=CE,∠BFA=∠DEC=90°,证得Rt△BFA≌Rt△DEC(HL),便知BF=DE;
(2)解法同(1).
(1)证明:∵DE⊥AC,BF⊥AC,
∴∠BFA=∠DEC=90°.
又∵AE=CF,
∴AE+EF=CF+EF,即AF=CE,
在Rt△BFA与Rt△DEC中,
![]() ,
,
∴Rt△BFA≌Rt△DEC(HL),
∴BF=DE,
(2)解:∵DE⊥AC,BF⊥AC,
∴∠BFA=∠DEC=90°.
又∵AE=CF,
∴AE﹣EF=CF﹣EF,即AF=CE,
在Rt△BFA与Rt△DEC中,
![]() ,
,
∴Rt△BFA≌Rt△DEC(HL),
∴BF=DE=3cm.


科目:初中数学 来源: 题型:
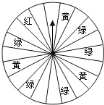
【题目】某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成![]() 份),并规定:顾客每购物满
份),并规定:顾客每购物满![]() 元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得
元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得![]() 元、
元、![]() 元、
元、![]() 元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得
元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得![]() 元的购物券.
元的购物券.
![]() 求转动一次转盘获得购物券的概率;
求转动一次转盘获得购物券的概率;
![]() 转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】海珠区某学校为进一步加强和改进学校体育工作,切实提高学生体质健康水平,决定推进“一人一球”活动计划. 学生可根据自己的喜好选修一门球类项目(A :足球,B:篮球,C:排球,D:羽毛球,E:乒乓球),陈老师对某班全班同学的
选课情况进行统计后,制成了两幅不完整的统计图 (如图).
(1) 求出该班的总人数,并将条形统计图补充完整;
(2) 若该校共有学生 2500 名,请估计约有多少人选修足球?
(3) 该班班委 4 人中,1 人选修足球,1 人选修篮球,2 人选修羽毛球,陈老师要从这
4 人中任选 2 人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求 选出的 2 人中至少有 1 人选修羽毛球的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年中秋节来期间,某超市以每盒80元的价格购进了1000盒月饼,第一周以每盒168元的价格销售了300盒,第二周如果单价不变,预计仍可售出300盒,该超市经理为了增加销量,决定降价,据调查,单价每降低1元,可多售出10盒,但最低每盒要赢利30元,第二周结束后,该超市将对剩余的月饼一次性赔钱甩卖,此时价格为70元/盒.
(1)若设第二周单价降低x元,则第二周的单价是 ______ ,销量是 ______ ;
(2)经两周后还剩余月饼 ______ 盒;
(3)若该超市想通过销售这批月饼获利51360元,那么第二周的单价应是多元?
查看答案和解析>>
科目:初中数学 来源: 题型:
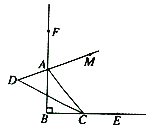
【题目】综合与探究
如图所示:点![]() 和点
和点![]() 分别在射线
分别在射线![]() 和射线
和射线![]() 上运动(点
上运动(点![]() 和点
和点![]() 不与点
不与点![]() 重合),
重合),![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 在顶点
在顶点![]() 处的外角平分线,
处的外角平分线,![]() 的反向延长线与
的反向延长线与![]() 交于点
交于点![]() .试回答下列问题:
.试回答下列问题:
(1)若![]() ,则
,则![]() _________
_________![]() ,若
,若![]() ,则
,则![]() _________
_________![]() .
.
(2)设![]() ,用
,用![]() 表示
表示![]() 的度数,则
的度数,则![]() __________
__________![]() .
.
(3)试猜想,点![]() 和点
和点![]() 在运动过程中,
在运动过程中,![]() 的度数是否发生变化?若变化,请求出变化范围;若不变,请给出证明.
的度数是否发生变化?若变化,请求出变化范围;若不变,请给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直角三角形三边长为a、b、c,则以下列线段为边长的三角形是直角三角形的是( )
A.a+2,b+2,c+2B.3a,4b,5cC.a+3,b+4,c+5D.2a,2b,2c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() 所示,
所示,![]() 为矩形
为矩形![]() 的边
的边![]() 上一点,动点
上一点,动点![]() 、
、![]() 同时从点
同时从点![]() 出发,点
出发,点![]() 以
以![]() 秒的速度沿折线
秒的速度沿折线![]() 运动到点
运动到点![]() 时停止,点
时停止,点![]() 以
以![]() 秒的速度沿
秒的速度沿![]() 运动到点
运动到点![]() 时停止.设
时停止.设![]() 、
、![]() 同时出发
同时出发![]() 秒时,
秒时,![]() 的面积为
的面积为![]() .已知
.已知![]() 与
与![]() 的函数关系图象如图
的函数关系图象如图![]() (其中曲线
(其中曲线![]() 为抛物线的一部分,其余各部分均为线段),则下列结论:①
为抛物线的一部分,其余各部分均为线段),则下列结论:①![]() ;②当
;②当![]() 时,
时,![]() ;③
;③![]() ;④当
;④当![]() 秒时,
秒时,![]() ;⑤当
;⑤当![]() 的面积为
的面积为![]() 时,时间
时,时间![]() 的值是
的值是![]() 或
或![]() ;其中正确的结论是________.
;其中正确的结论是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某送奶公司计划在三栋楼之间建一个取奶站,三栋楼在同一条直线,顺次为A楼、B楼、C楼,其中A楼与B楼之间的距离为40米,B楼与C楼之间的距离为60米.已知A楼每天有20人取奶,B楼每天有70人取奶,C楼每天有60人取奶,送奶公司提出两种建站方案.
方案一:让每天所有取奶的人到奶站的距离总和最小;
方案二:让每天A楼与C楼所有取奶的人到奶站的距离之和等于B楼所有取奶的人到奶站的距离之和.
(1)若按照方案一建站,取奶站应建在什么位置?
(2)若按照方案二建站,取奶站应建在什么位置?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com