
【题目】某农场去年种植了10亩地的南瓜,亩产量为2000kg,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,设南瓜种植面积的增长率为x.
(1)则今年南瓜的种植面积为 亩;(用含x的代数式表示)
(2)如果今年南瓜亩产量的增长率是种植面积的增长率的![]() ,今年南瓜的总产量为60000kg,求南瓜亩产量的增长率.
,今年南瓜的总产量为60000kg,求南瓜亩产量的增长率.
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】二次函数![]() (a≠0)图象如图所示,下列结论:①abc>0;②2a+b=0;③当m≠1时,a+b>
(a≠0)图象如图所示,下列结论:①abc>0;②2a+b=0;③当m≠1时,a+b>![]() ;④a-b+c>0;⑤若
;④a-b+c>0;⑤若![]() , 且
, 且![]() , 则
, 则![]() .其中正确的有( ).
.其中正确的有( ).
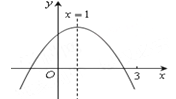
A. ①②③ B. ②④ C. ②⑤ D. ②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新华商场为迎接家电下乡活动销售某种冰箱,每台进价为2500元,市场调研表明;当销售价定为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台,商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着城际铁路的正式开通,从甲市经丙市到乙市的高铁里程比普快里程缩短了90km,运行时间减少了8h,已知甲市到乙市的普快列车里程为1220km.高铁平均时速是普快平均时速的2.5倍.
(1)求高铁列车的平均时速;
(2)某日王先生要从甲市去距离大约780km的丙市参加14:00召开的会议,如果他买到当日9:20从甲市到丙市的高铁票,而且从丙市火车站到会议地点最多需要1小时.试问在高铁列车准点到达的情况下,它能否在开会之前20分钟赶到会议地点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成![]() 份),并规定:顾客每购物满
份),并规定:顾客每购物满![]() 元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得
元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得![]() 元、
元、![]() 元、
元、![]() 元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得
元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得![]() 元的购物券.
元的购物券.
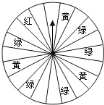
![]() 求转动一次转盘获得购物券的概率;
求转动一次转盘获得购物券的概率;
![]() 转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与y轴交于点A(0,2),对称轴为直线x=﹣2,平行于x轴的直线与抛物线交于B、C两点,点B在对称轴左侧,BC=6.
(1)求此抛物线的解析式.
(2)点P在x轴上,直线CP将△ABC面积分成2:3两部分,请直接写出P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图所示:点![]() 和点
和点![]() 分别在射线
分别在射线![]() 和射线
和射线![]() 上运动(点
上运动(点![]() 和点
和点![]() 不与点
不与点![]() 重合),
重合),![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 在顶点
在顶点![]() 处的外角平分线,
处的外角平分线,![]() 的反向延长线与
的反向延长线与![]() 交于点
交于点![]() .试回答下列问题:
.试回答下列问题:
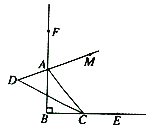
(1)若![]() ,则
,则![]() _________
_________![]() ,若
,若![]() ,则
,则![]() _________
_________![]() .
.
(2)设![]() ,用
,用![]() 表示
表示![]() 的度数,则
的度数,则![]() __________
__________![]() .
.
(3)试猜想,点![]() 和点
和点![]() 在运动过程中,
在运动过程中,![]() 的度数是否发生变化?若变化,请求出变化范围;若不变,请给出证明.
的度数是否发生变化?若变化,请求出变化范围;若不变,请给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com