
【题目】临近端午节,某食品店每天卖出300只粽子,卖出一只粽子的利润为1元.经调查发现,零售单价每降0.1元,每天可多卖出100只粽子.为了使每天获得的利润更多,该店决定把零售单价下降m(0<m<1)元,
(1)零售单价降价后,每只利润为 元,该店每天可售出 只粽子.
(2)在不考虑其他因素的条件下,当零售单价下降多少元时,才能使该店每天获取的利润是420元,且卖出的粽子更多?
【答案】(1) (1-m) ,(300+1000m);(2)当零售单价下降0.4元时,才能使该店每天获取的利润是420元,且卖出的粽子更多
【解析】
(1)降价后的利润等于原来的利润-降价即可得到;每天的销售量等于原有销售量加上增加的销售量即可;
(2)利用总利润等于销售量乘以每件的利润即可得到方程求解.
(1)该店每天可售出300+100×![]() =(300+1000m)只粽子.
=(300+1000m)只粽子.
每只利润为(1-m)元;
(2) 根据题意,得(1-m)(300+1000m)=420,
解得m1=0.4 m2=0.3,
显然,当m=0.4时, 300+1000m=700,
当 m=0.3时, 300+1000m=600,
700>600,
答:当零售单价下降0.4元时,才能使该店每天获取的利润是420元,且卖出的粽子更多.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC的平分线与BC边的垂直平分线相交于点P,过点P作AB、AC(或延长线)的垂线,垂足分别是M、N,求证:BM=CN. 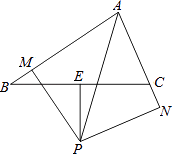
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
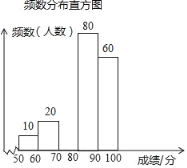
【题目】某校组织了全校1500名学生参加传统文化知识网络竞赛.赛后随机抽取了其中200名学生的成绩作为样本进行整理,并制作了如下不完整的频数分布表和频数分布直方图.
成绩(分) | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | n |
70≤x<80 | m | 0.15 |
80≤x<90 | 80 | 0.40 |
90≤x<100 | 60 | 0.30 |
请根据图表提供的信息,解答下列各题:
(1)表中m= ,n= ,请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段80≤x<90对应扇形的圆心角的度数是 ;
(3)若成绩在80分以上(包括80分)为合格,则参加这次竞赛的1500名学生中成绩合格的大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
(1)有理化因式:两个含有根式的非零代数式相乘,如果它们的积不含有根式,那么这两个代数式相互叫做有理化因式.例如:![]() 的有理化因式是
的有理化因式是![]() ;
;![]() 的有理化因式是
的有理化因式是![]() .
.
(2)分母有理化:分母有理化又称“有理化分母”,也就是把分母中的根号化去.指的是如果代数式中分母有根号,那么通常将分子、分母同乘以分母的有理化因式,达到去分母中根号的目的.如:![]() ,
,![]()
问题解决:
(1)填空:![]() 的有理化因式是______.(x≥1)
的有理化因式是______.(x≥1)
(2)直接写出下列各式分母有理化的结果:
①![]() _____;②
_____;②![]() ______.
______.
(3)计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c的顶点为B(﹣1,3),与x轴的交点A在点(﹣3,0)和(﹣2,0)之间,以下结论:
①b2﹣4ac=0;②a+b+c>0;③2a﹣b=0;④c﹣a=3
其中正确的有( )个.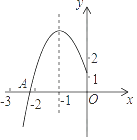
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家![]() 妈妈8:30从家出发,乘车沿相同路线去姥姥家
妈妈8:30从家出发,乘车沿相同路线去姥姥家![]() 在同一直角坐标系中,小亮和妈妈的行进路程与北京时间的函数图象如图所示,根据图象得到如下结论,其中错误的是
在同一直角坐标系中,小亮和妈妈的行进路程与北京时间的函数图象如图所示,根据图象得到如下结论,其中错误的是![]()
![]()
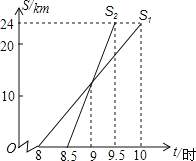
A. 9:00妈妈追上小亮B. 妈妈比小亮提前到达姥姥家
C. 小亮骑自行车的平均速度是![]() D. 妈妈在距家13km处追上小亮
D. 妈妈在距家13km处追上小亮
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,AG⊥BG,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°.其中正确的结论是( )
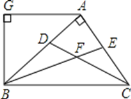
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B,分别向上平移2个单位,再向右平移1个单位,分别得到点A、B的对应点C、D,连接AC,BD,CD,得平行四边形ABDC.
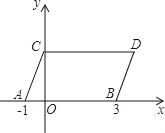
(1)直接写出点C,D的坐标;
(2)若在直线CD上存在点M,连接MA,MB,使S△MAB=2S△MBD,求出点M的坐标;
(3)若点P在直线BD上运动,连接PC,PO,请画出图形,写出∠CPO,∠DCP,∠BOP的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com